PCA降维

[TOC]

1.起因

PCA，又叫Principal Component Analysis，即主成分分析，为什么要这么说呢，他实际上是通过降维的方法，保留数据的主要成分，同时又降低了储存和计算的困难

为什么可以通过这种降维的方法达到目的？因为现实生活中我们遇到的很多数据，虽然具有很高的维度，但是他们往往维度不是相互独立的，也就是说，我们只需要用其中的一些维度就能把其他维度很好的表示出来，如:

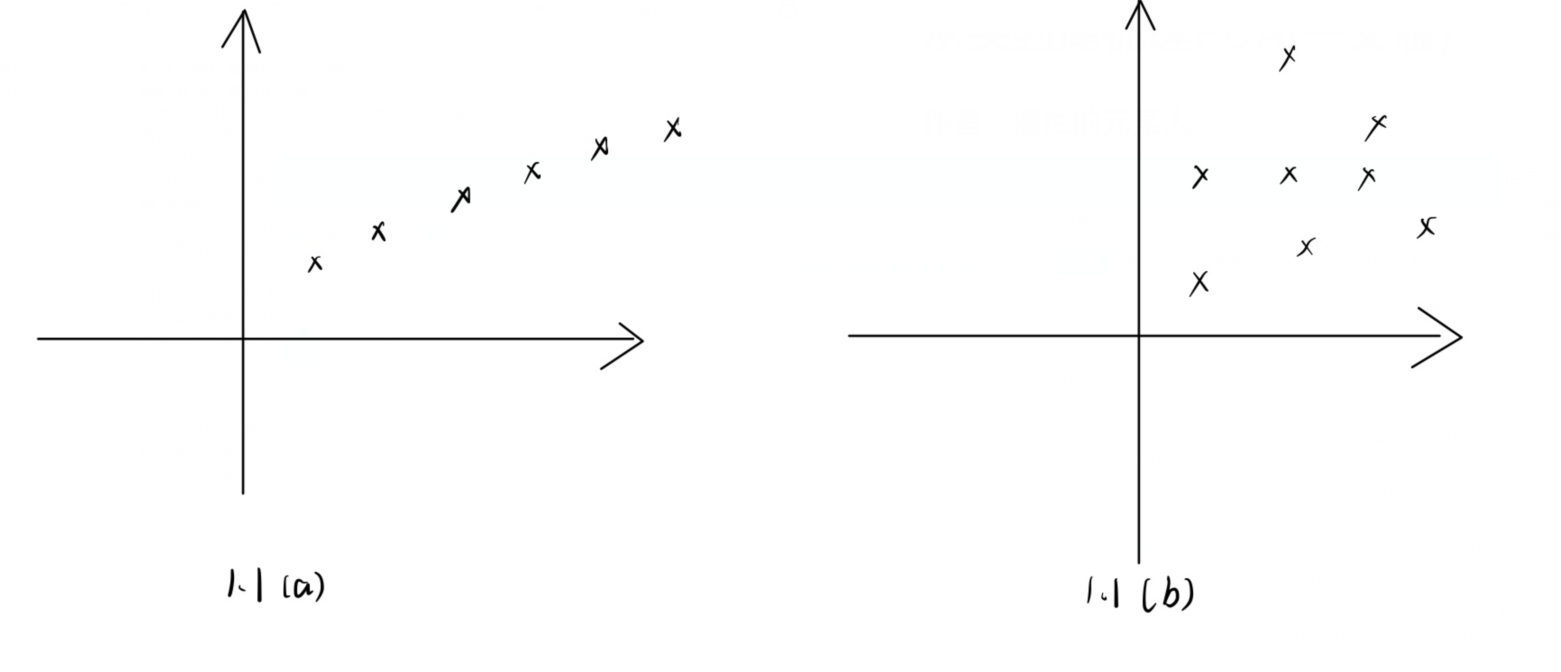
1.1(a) 的坐标轴中的数据点上可以直观的看出x和y是有着线性关系的，而 (b) 部分很难直接观察出两者的关系，这种情况降维就不可用(也许该数据在更高维度上是可分或者有着其他关系，这需要用到核函数进行维度扩展)

那么PCA如何对类似(a)的情况(乃至更多维度向下)进行降维呢？
PCA只考虑线性关系进行降维，这种线性降维的问题也被看做如何找到线性约束或者发现$R^D$的低维子空间的过程

2.线性降维的实现:基变换

现在考虑这样的一个简单等式:

$$x^T\omega +b=0$$

其表示了$x\in R^D$各分量之间的线性关系.
但是我们知道，满足该公式的$x$位于$R^D$的一个维数为$D-1$的子空间中？
为什么： 举例来说，对于一维$ax+b=0$的情况，其结果为二维上的一条直线

2.1 基变换：矩阵变换

我们说，降维实质上是一种基变换，先给出基变换的说明，为了通俗，我直接给出以下例子(默认的，我们知道原本的坐标实际上是以$(1,0),(0,1)$为基的表示)
将$(1,1),(2,2),(3,3)$扩展到以$(1/\sqrt{2},1/\sqrt{2})$和$(-1/\sqrt{2},,1/\sqrt{2})$为基的矩阵，是做出以下矩阵变换:

$$\left[ \begin{matrix} 1/\sqrt{2} &1/\sqrt{2}\\ -1/\sqrt{2} &1/\sqrt{2} \end{matrix} \right] \left[ \begin{matrix} 1& 2 & 3\\ 1 & 2 &3\\ \end{matrix} \right] =\left[ \begin{matrix} \sqrt{2}&2\sqrt{2}&3\sqrt{2} \\ 0&0&0\\ \end{matrix} \right]$$

我们将坐标进行了如上面所示的基变换，可以看到结果里坐标的第二个维度信息变换成了0，如果我们将其除去，也就变相的完成了降维(也就是只用$(1/\sqrt{2},1/\sqrt{2})$一个基来表示)
下面我们给出更为正式的定义:我们想要将M个N维向量($a_1-a_M$)变换到R个N维向量的空间($P_1-P_R$)中，这里的R在降维下显然是小于N的:

$$\begin{pmatrix} P_1 \\ ... \\ P_R \end{pmatrix}\begin{pmatrix} a_1 & ... & a_M \end{pmatrix}=\begin{pmatrix} P_1a_1 & ... & P_1a_M \\ P_2a_1 & ... & P_1a_M\\ ... & ... & ...\\ P_Ra_1 & ... & P_Ra_M \end{pmatrix}$$

这里可以给出矩阵相乘的定义:两个矩阵相乘，实际上是将右边矩阵的列向量变换到左边矩阵行向量为基的空间中，因此产生了降维(新的矩阵向量是R维的)

3.PCA降维实现

3.1 降维到零维子空间

零维是一个没有长宽高的点，因此样本点仅仅表示其存在与否
对于一组样本点$X=\{x_1,x_2,..,x_n\}$，我们要用零维降维表示这些样本点，那么在降维后必有$x^=x_1=x_2=…=x_n$(零维点)
如果没有噪声，其实非常简单，每个降维后的样本点都相同，如上面所示，但是若存在噪声，它们就不一定相等了，这时候我们仍然需要考虑找到一个向量$x^$作为X中元素的零维表示
假设噪声很小，那么m和$x_i$之间的差距其实很小，那么自然的，我们产生了最小化其到X中所有距离的可能性，当噪声为0，这个值为0 。
形式化的，我们有如下:

$$x_{best}=argmin_{x} \frac{1}{N}\sum_{i=1}^N||x_i-x^*||^2=J(x^*)$$

根据$||x_i-x^||^2=(x_i-x^)^T(x_i-x^)$
,以及$\frac{\partial x^Tx}{\partial x}=2x$
对所给求导得到$\frac{J(x^)}{x^}=\frac{2}{N}\sum_{i=1}^N(x^-x_i)$
得到最佳的$x^=\frac{1}{N}\sum_{i=1}^Nx_i=\overline{x}$，
即降维到零维表示的最佳向量为$x^=\overline{x}$:x的均值

3.2 降维到一维子空间(推广就是超平面)

一维子空间是一条直线，因此形式化的，我们可以知道即是将一些高维的样本点投射到一条直线上，直觉的，我们有如下目标:
1.样本点投射到直线上的距离尽可能短
2.样本点在直线上之间的距离尽可能长

3.2.1 样本中心化:减去均值

中心化的作用如下:对于线性降维$y=a^Tx+b$，由于有b的存在，假如我们没有中心化，我们所需要降维的结果为:

但是由于我们降维过程中是没有b的，最后形成的线性变换会是如下结果: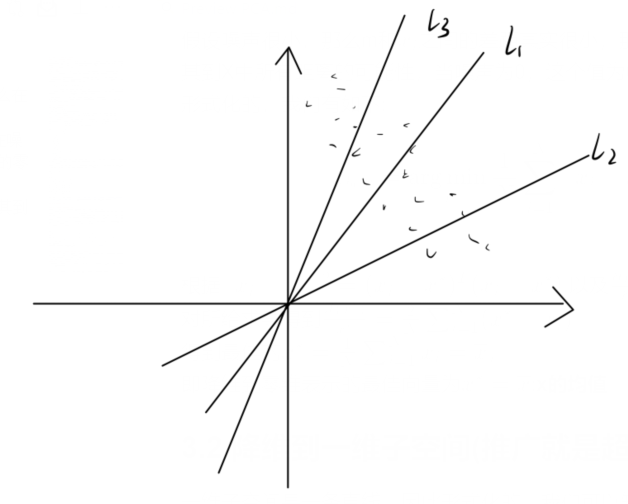

显然不是我们需要的结果，因此去中心化的目的:消除数据的平移影响，如本图，在去中心化之后会得到大致如下的降维结果: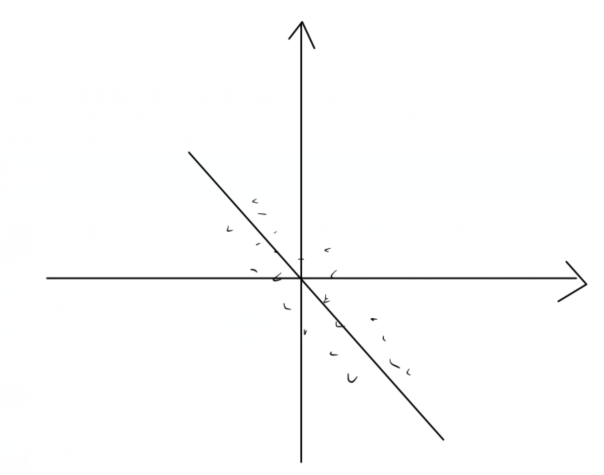

显然这是我们需要的

3.2.2 降维过程-1

对于上面我们讲的两个目标，从两个目标出发有两个异曲同工的想法，这里先说比较容易理解的第二个:要让样本点在这个直线上的投影点之间的距离尽可能长，自然的想到了让降维之后的样本点方差足够的大
对于每一个$x_i$，在去中心化之后线性降维的结果为$\omega^T(x_i-\overline{x})$(中心化之后均值为0)，这也就是我在2.1部分所说的基变换:矩阵变换
因此，我们自然的想要最大化:$\frac{1}{N}\sum_{i=1}^N||\omega^T(x_i-\overline{x})||^2$,形式化有如下表达:

$$argmax_{\omega} \quad J_1(\omega)=\frac{1}{N}\sum_{i=1}^N||\omega^T(x_i-\overline{x})||^2\\ s.t. \quad \omega^T\omega=1$$

约束条件我们后面再说。
对于$J_1(\omega)$，有$J_1(\omega)=\frac{1}{N}\sum_{i=1}^N||\omega^T(x_i-\overline{x})||^2=\omega^T[\frac{1}{N}\sum_{i=1}^N(x_i-\overline{x})(x_i-\overline{x})^T]\omega=\omega^TCov(x)\omega$

对上面的约束使用Lagrange乘子法:

$$f(\omega,\lambda)=\omega^TCov(x)\omega-\lambda(\omega^T\omega-1)$$

我们有:$\frac{\partial f}{\partial \omega}=0$,$\frac{\partial f}{\partial \lambda}=0$
因此得到:

$$2Cov(x)\omega-2\lambda\omega=0$$, $$\omega^T\omega=1$$

从

$$Cov(x)\omega=\lambda\omega$$

你想到了什么？特征值和特征向量!没错，这正是解得的用意:$\lambda$即是特征值，而$\omega$即所求特征向量
选择$\lambda_1$对应的最大特征值作为特征向量$\omega$即可做到最大化结果!

-证明$Cov(x)$半正定-

$$\begin{align*} &Cov(x)=\frac{1}{N}\sum_{i=1}^N(x_i-\overline{x})^2\\ &a Cov(x)a^T=a·E[(x_i-\overline{x})(x_i-\overline{x})^T]·a^T\\ &=E[a(x_i-\overline{x})(a(x_i-\overline{x}))^T]=E[(a(x_i-\overline{x}))^2]\geq 0 \end{align*}$$

3.2.3 降维过程-2

这里我们最小化投影点到原来样本点之间的距离来进行问题求解，最后可以得到这种方法和3.2.2的结果是相同的
这里的思想其实类似于零维的时候，假设我们降维前的结果为$x_i$，对于投影，实际上降维后的向量为$a\omega_1+x_0$，其中$\omega$是方向，$a$是长度标量，如下面所示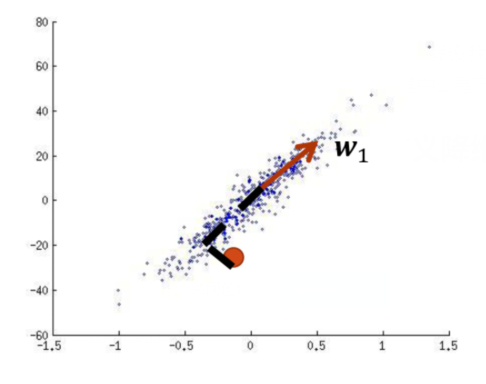

-投影说明-

由于数学知识我们知道,一个向量$y$向另一个方向的向量$x$上的投影结果为$\frac{y^Tx}{||x||^2}x$，在本题中即是$\omega_1^T(x-\overline{x})\omega_1$(其中$\omega_1^T\omega_1=1$，前面的内积是标量做转置不影响结果)
即：$x\approx \overline{x}+(\omega_1^T(x-\overline{x}))\omega_1$,其中$y_i=\omega_1^T(x-\overline{x}),b=\overline{x}$
回到上面的结果，我们需要最小化投影前后样本点之间的距离,即:

$$\begin{align*} J_2(\omega)&=\frac{1}{N}\sum_{i=1}^N||x_i-(\overline{x}+a_i\omega)||^2\\ & =\frac{1}{N}\sum_{i=1}^N||a_i\omega-(x_i-\overline{x})||^2\\ &=\sum_{i=1}^N\frac{a_i^2||\omega||^2+||x_i-\overline{x}||^2-2a_i\omega^T(x-\overline{x})}{N} \end{align*}$$

对其，我们需要知道的是投影方向$\omega$和每个样本的投影长度$a_i$，对其计算偏导数有:

$$\frac{\partial J}{\partial \omega}=\frac{2}{N}\sum_{i=1}^N(a_i^2\omega-a_i(x-\overline{x}))=0$$ $$\frac{\partial J}{\partial a_i }=\frac{2}{N}(a_i||\omega^2||-\omega^T(x-\overline{x}))=0$$

得到$a_i=\frac{\omega^T(x_i-\overline{x})}{||\omega^2||}$,即$a_i$的最优值是将$x_i-\overline{x}$投影到$\omega$方向上之后带符号的长度(和前面的投影做对比即可)
而我们对$a_i\omega=\frac{\omega^T(x_i-\overline{x})\omega}{||\omega^2||}=\frac{(c\omega)^T(x_i-\overline{x})(c\omega)}{||c\omega^2||}$,即我们对投影方向$\omega$做任意的长度变换不会影响最后的结果，也因此我们可以指定$||\omega||=1$便于化简计算
这时候$a_i=\omega^T(x_i-\overline{x})=\omega(x_i-\overline{x})^T$
代回到原式:

$$\begin{align*} J_2(\omega,a)&=\frac{1}{N}\sum_{i=1}^N(a_i^2||\omega||^2+||x_i-\overline{x}||^2-2a_i\omega^T(x-\overline{x}))\\ &=\frac{1}{N}\sum_{i=1}^N(||x_i-\overline{x}||^2-a_i^2) \end{align*}$$

由于$||x_i-\overline{x}||^2$和$\omega,a$无关，因此我们的最后目标变成了最大化$\frac{1}{N}\sum_{i=1}^Na_i^2$
现在我们转向刚刚没有用到的式子

$$\frac{\partial J}{\partial \omega}=\frac{2}{N}\sum_{i=1}^N(a_i^2\omega-a_i(x-\overline{x}))=0$$

它告诉我们:$\frac{1}{N}(\sum_{i=1}^Na_i^2)\omega=\frac{1}{N}\sum_{i=1}^Na_i(x-\overline{x})=\frac{1}{N}\sum_{i=1}^N((x-\overline{x})a_i)=Cov(x)\omega$(这和上一种相同)
因此，我们想要最大化的结果，就是对应的$Cov(x)$的特征向量的特征值(最大的特征值，这与之前不谋而合!)

3.3 PCA的推广实现(广义降维,暂略)

4.注意事项

4.1 对于$J_2(\omega,a)$的说明

根据之前$J_2(\omega,a)$的判别式可以看到$J_2(\omega,a)=J_2(c\omega,a/c)$，因此$J_2(\omega/||\omega||,a||\omega||)$，因此如果$J_2(\omega^,a^)$是最优解，$J_2(c\omega^,a^*/c)$也是最优解(这里的a为所有a整体的行向量)
因此我们可以指定$\omega=1$,在不改变优化目标的时候化简过程，这也与直觉相适应(因为$\omega$只控制方向，大小由$a_i$控制)

5.参考书籍

机器学习:zzh

模式识别:wjx

南瓜书