Resume

Show yourself

0%

第二周附加内容

发表于 更新于 分类于
第二周的附加内容，代码实现：一个多维线性回归应该如何实现的整体思路和代码框架

一.预先说明

数据的规模不限，表示的形式为如下形式：

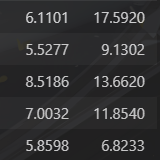
每一行是一个数据，行数即为数据的数目，列数为数据的维度(最后一行为标记)

目的是做回归直线来拟合数据的点，并最小化loss

二.代码实现

由于原理在week1和2中已经有了详尽的说明，这里只给出代码实现的框架并且给出一定的解释。

2.1 数据的提取和预处理

1
2
3
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

读取数据并进行预处理

header不设置或者为None就是默认的0-1标签，设置为n把n+1行的数字当成标签(路径需要注意)

data.head()可以默认展示前五行的数据

1
data=pd.read_csv("data.txt",header=None)

可以画散点图观察数据的分布，但是仅限维度情况

1
2
data.plot(kind='scatter', x='one class', y='the other class', figsize=(12,8))
plt.show()

下面开始对数据进行处理

*可能的操作：对变量进行归一化处理

  • Min-Max标准化:将样本数据等比例缩放到一个特定的范围 [a,b] 之内,常用的缩放区间是 [0, 1]

    1
    data=(data - min(data)) / (max(data) - min(data))

    这种方法的实现细节还需要再考虑

  • Z-score:这种方法的范围是整个实数集，将数据变换为均值为0，标准差为1的分布，但不是传统意义的归一化

    1
    data = (data-data.mean())/data.std()

首先要将标签和数据进行分离，这里假设X是训练数据，y是标签

1
2
3
column=data.shape[1]#数据第二维度数，即每条数据的列数目
X=data.iloc[:,0:column-1]#除了最后的所有列
y=data.iloc[:,column-1:column]

在0处添加全1列，名称为ones，理由后面会说

1
X.insert(0, 'Ones', 1)
  • 注意这里的添加需要在X被转化成matrix之前，否则会出现：‘matrix’ object has no attribute ‘insert’

其次注意这个数据的类型是dataFrame的，要先转化成np.matrix才方便进行处理（.values是取值，但是好像不加也可以获得相同的效果）

1
2
X=np.matrix(X.values)
y=np.matrix(y.values)

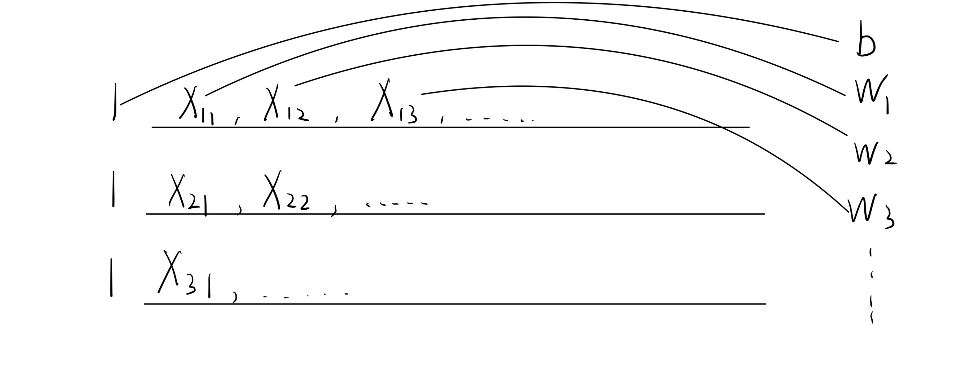
假设变量为$\vec{w}$，那么我们需要一个长度为data.shape[1]+1的向量$\vec{w}$作为未知量进行参数更新，其中$\vec{w}=[b,w_1,w_2,…]$

这样做的好处是，我们只需要更新$w$即可，b会放在里面一起更新

但是同时意味着，我们需要对X加上一层处理：在所有数据前加上统一的1（或者数据的最后或者任意的位置，只要保持一致即可，因为在线性函数中，常数项的位置是任意的）

1
w=np.matrix(np.array([0]*X.shape[1]))
  • w直接设成初始值即可，注意这里因为是在添加全1列之后，因此只需要设置成X.shape[1]即X的特征数目即可

至此，我们完成了所有的数据预处理

2.2 计算

我们需要先进行以下框架说明：

  • 首先，我们需要计算X和w的乘积，这是预测的$\hat{y}$，接着我们需要把预测的$\hat{y}$和真实的y做对比，得到损失函数
  • 在损失函数的基础上进行梯度下降回归，对参数w进行更新，注意在这种方法下所有的w要同时更新
  • 不断重复，直到达到预期的损失足够小或者一定的迭代次数

损失函数计算：

  • 可能的损失函数种类：平方损失，Hinge损失，对数损失…
  • 这里选用平方:$\frac{1}{2m}\sum_{i=1}^m(\hat{y}-y)^2$
1
2
3
4
5
def cost_function(X,y,w):
    predict_y=np.dot(X,w.T)
    square=np.power(predict_y-y,2)
    m=X.shape[0]
    return np.sum(square)/(2*m)

设置学习率和迭代次数，前者是步长后者是循环次数，复杂的时候还会对比损失函数的值

1
2
iters=1500
alpha=0.01

先计算一下当前的损失

1
float(cost_function(X,y,w))

在前面的基础上进行梯度下降:$w_i:=w_i-\alpha\frac{1}{m}\sum_{i=1}^m(\hat{y}_i-y_i)x_i$

  • 这里也体现了前面全1列的好处：1可以直接放进去更新而不影响整体
  • 这里选择的批量梯度下降，每次都把所有样本放进去下降
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def gradient_descent(X,y,w,alpha,iters):
    #temp矩阵用于存w的临时值，方便一起更新
    #temp=np.matrix(np.array([0]*X.shape[1]))
    temp = np.matrix(np.zeros(w.shape))
    #记录损失曲线可以可视化损失函数,先建立一个全0数组
    loss=np.zeros(iters)
    i=0
    parameter=w.shape[1]
    while i<iters:
        error=np.dot(X,w.T)-y
        for j in range(parameter):
            #error和 X[:,j]即第j列逐元素相乘
            descent=np.multiply(error,X[:,j])
            #用这个表示是因为temp为matrix类型
        	temp[0, j] = w[0, j]-alpha/X.shape[0]*np.sum(descent)
        w=temp
        cost[i]=cost_function(X,y,w)
        i+=1

接下来就是进行测试

1
2
para,cost=gradientDescent(X,y,theta,alpha,iters)
float(cost_function(X, y, para))
  • 0.130686706060959

损失函数图

1
2
3
4
5
6
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters), cost, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()

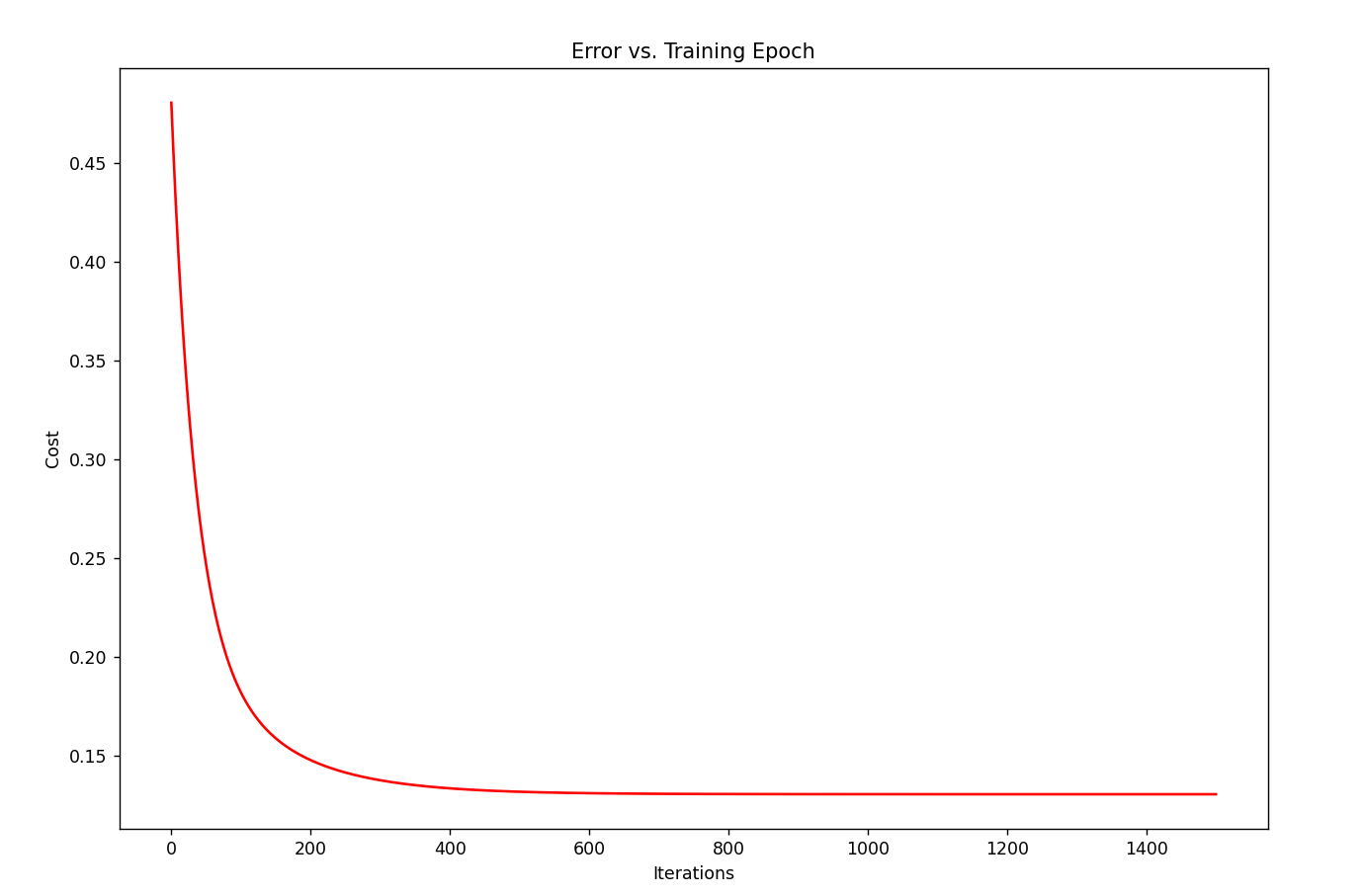
至此完成一个模型的结构

主要难点：理解和梯度下降