摘要
增量学习遇到的问题:
1) adequately address the class bias problem
类别不平衡
2) alleviate the mutual interference between new and old tasks
新旧任务之间的干扰
3) consider the problem of class bias within tasks.
任务内的偏差
1.介绍
可能解决增量学习的方法:
memory storage replay [Ahn et al., 2021; Li and Hoiem, 2017; Wu et al., 2019; Rebuffi et al., 2017; Yan et al., 2021]
- 储存过去的记忆或者模拟人类的记忆
- 由于隐私限制和内存规模优先,旧数据的访问稀缺
- 出现问题:任务类间偏差\类别不平衡问题
- severe inter-task class bias, or known as the class imbalance issue between old and new tasks.
- recent approaches [Ahn et al., 2021; Rebuffi et al., 2017; Yan et al., 2021]
- utilizing rescaling 重新缩放
- balanced scoring 平衡分数
- softmax separating softmax分离
- 类别不平衡的问题依然存在,新旧任务之间的干扰没有解决…
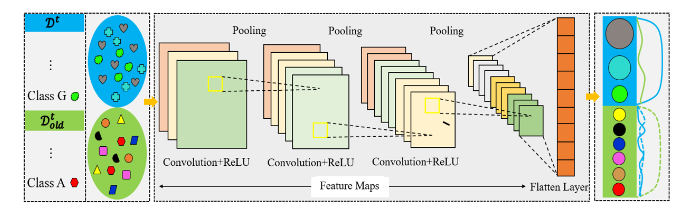
深度学习模型在面对类不平衡和互相干扰问题时的情况图中通过图像和文字说明了以下几个关键点:
类不平衡问题(Class Imbalance Issues):
- 左边的图展示了两个数据集 $ D^t $(新任务的训练数据)和 $D^{t-1}$(旧任务的训练数据)。在新任务中,不同类别的数据分布不均,比如类别 G 拥有较多样本(绿色圆圈),而类别 A 样本较少(红色三角形)。这类不平衡会导致模型的神经元对数据量多的类别有偏向性。
- 类不平衡也体现在每个任务内部和任务之间,这会导致完全连接层(图中的右侧层)中的权重偏差,进而影响模型的学习效果。
互相干扰问题(Mutual Interference Issues):
- 右侧展示了卷积神经网络的多层特征提取过程,包括卷积层(Convolution+ReLU)、池化层(Pooling),并最终通过全连接层(Flatten Layer)进行分类。
- 图中蓝色的线条表示了在更新新任务模型时,旧任务的输出结果应趋近于 0(旧任务的输出应不再影响新任务的分类),但实际中,旧任务的分类头(classification heads)输出可能仍然较大,甚至干扰到新任务的分类。这被称为遗忘问题(catastrophic forgetting),即在训练新任务时,模型对旧任务的表现可能变得不稳定或不准确。
模型更新前后(Before and After Model Update):
- 图中用蓝色虚线和实线来表示模型更新前后输出的变化。虚线表示新任务数据在旧任务分类头中的表现(应为零或接近零),而实线表示更新后的情况,模型对旧任务的表现变得不一致,这体现了连续学习中的互相干扰问题。
model dynamic expansion [Serra et al., 2018; Mallya and Lazebnik, 2018]
regularization constraints design [Aljundi et al., 2019]
本文贡献:a joint input and output coordination (JIOC) mechanism, which enables incremental learning models to simultaneously alleviate the class imbalance and reduce the interference between the predictions of old and new tasks.
方法:different weights are adaptively assigned to different input data according to their gradients for the output scores during the training of the new task and updating of the old task models. Then the outputs of old task data on new classification heads are explicitly suppressed and knowledge distillation (KD) [Menon et al., 2021] is utilized for harmonization of the output scores based on the principle of human inductive memory [Williams, 1999; Redondo and Morris, 2011].
- 不同类样本根据梯度甲醛,旧任务数据在新分类头上的输出背明确抑制,利用知识蒸馏(KD)协调输出梯度
knowledge distillation (KD) [Menon et al., 2021]
the principle of human inductive memory [Williams, 1999; Redondo and Morris, 2011]
2.相关工作
2.1 增量学习
定义为以下的模型:
- 模型可以从新的任务数据中学到有用的知识
- 旧的数据不需要访问或者只具有很少的访问权限
- 对所学的知识有记忆能力
-incremental learning [Mirza et al., 2022; Garg et al., 2022; Mallya et al., 2018],
-class-incremental learning [Ahn et al., 2021; Rebuffi et al., 2017; Yan et al., 2021; Zhang et al., 2020; Liu et al., 2021]
-small sample incremental learning [Tao et al., 2020; Cheraghian et al., 2021].
class-incremental learning (CIL), and most of these works overcome catastrophic forgetting by using knowledge distillation (KD) together with a small amount of old task data accessed.
-DMC [Zhang et al., 2020] utilizes separate models for the new and old classes and trains the two models by combining double distillation.
-SPB [Liu et al., 2021] utilizes cosine classifier and reciprocal adaptive weights, and a new method of learning class-independent knowledge and multi-view knowledge is designed to balance the stability-plasticity dilemma of incremental learning
- 没有解决任务内的类偏差和新旧任务的类偏差,这是本文的贡献:环节类不平衡并减少新旧任务预测之间的干扰
2.2 人类的归纳记忆
-Fisher et al. [Fisher and Sloutsky, 2005] demonstrated that category- and similarity-based induction should result in different memory traces and thus different memory accuracy. Hayes et al. [Hayes et al., 2013] examined the development of the relationship between inductive reasoning and visual recognition memory, and demonstrated it through two studies. Inspired by human inductive memory, Geng et al. [Geng et al., 2020] proposed a Dynamic Memory Induction Network (DMIN) to further address the small-sample challenge
3 方法
3.1 符号:CIL class Incremental Learning
新任务数据的持续到来:$D=\{D^1,D^2,…,D^t,…,D^T\}$
第t个新任务($D^t$)中的数据为$D^t=\{(x^t_{i,j},y^t_{i,j})_{i=1,2,…,m;j=1,2,…,n_m}\}$,其中m是类别数,$n_m$是第m个类别数内的样本数目,x是输出数据,y是对应的标签
当学习到新任务的时候,我们假设有一少部分旧任务数据仍然储存,如:$D_{old}^t=\{(x^1_{i,j},y^1_{i,j}),…,(x^t_{i,j},y^t_{i,j})\}$其中 $i=1,2,..,m;j=1,2,…,n_{old}\ll n$
在CIL中,特征提取器$f(·)$(举例:ResNet [He et al., 2016]))和一个全连接层(FCL)带有一个softmax分类器会是如下形式:
$X^{\tau}_{i,j}=f(x^{\tau}_{i,j};\Theta)$
$\hat{P}^{\tau}_{i,j}=softmax(x^{\tau}_{i,j};W)$
其中,$\tau=\{1,2,…,t\}$是特征提取器的参数,W是分类器的参数,$hat{P}^{\tau}_{i,j}$是输出分数的向量
当增量学习到第t个任务的时候,所有数据($D^t\cup D^t_{old}=(x^{\tau}_{i,j},y^{\tau}_{i,j}) $)都用于训练
并且经常采用交叉熵损失:
$L_{ce,t}=-\frac{1}{N_{old}+n_{new} }\sum_{i,j,k,\tau=1}^ty^{\tau}_{i,j,k}log(\hat{p}^{\tau}_{i,j,k})$
其中,$N_{old}$是旧任务存储下来的数据,$n_{new}$是新任务的所有样例,$\hat{p}^{\tau}_{i,j,k}$是第k个神经元的输出分数
3.2 概述
从上面可以知道,由于我们每次只能保存一小部分的旧任务的样本,而新样本的数目很大,因此在新旧任务之间会产生类别不平衡
新任务本身内部也可能会产生类别不平衡,但是现有的方法忽略了这一点
this is ignored by existing CIL approaches [Ahn et al., 2021; Rebuffi et al., 2017; Yan et al., 2021].
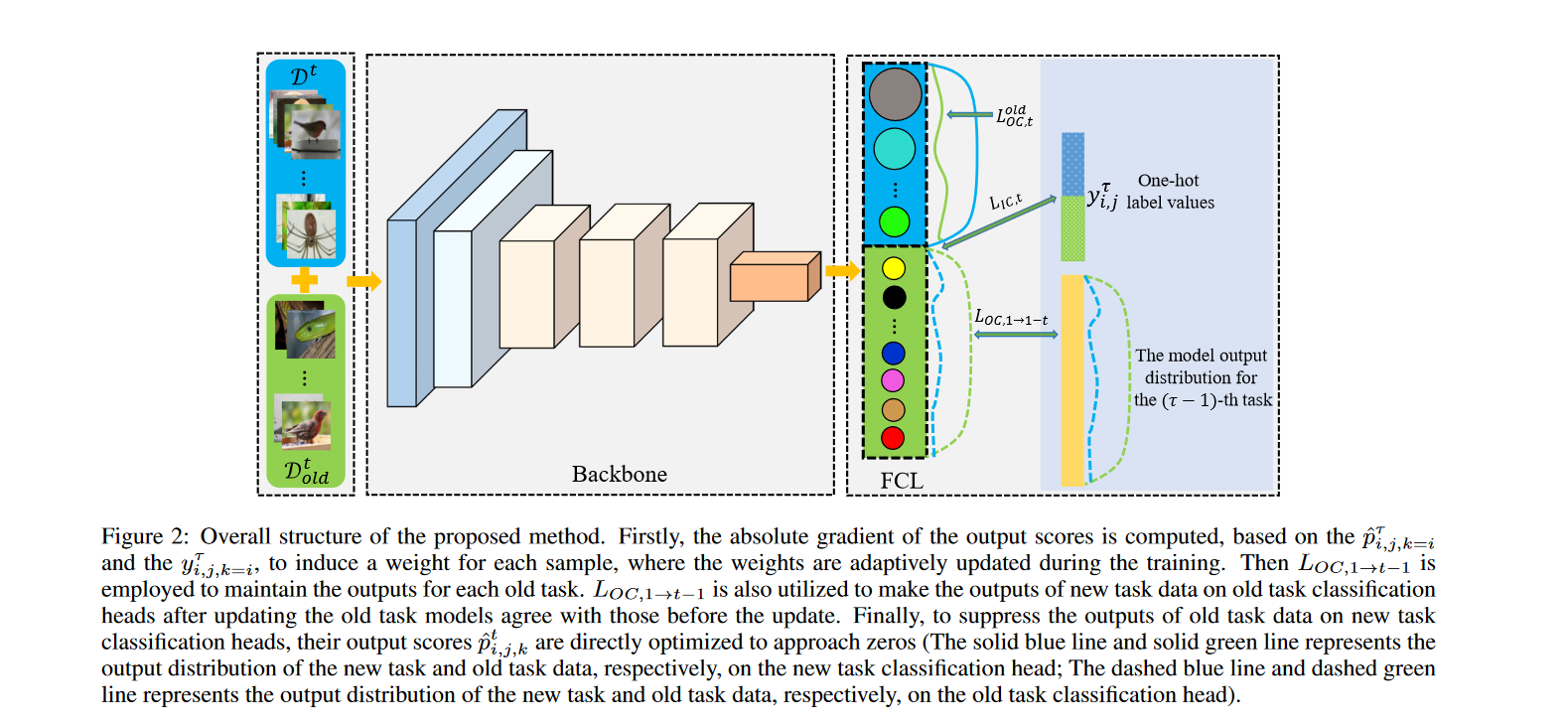
如图二所示,我们对不同的输入数据指派不同的权重,根据他们的输出分数的梯度;除此之外,我们拆分了softmax层inspired by the principle of human inductive memory.(类似SSIL [Ahn et al., 2021] approach,但是有几个显著的差异:1) for each of the old tasks, we utilize KD to maintain the output distribution of each task. To make the output scores of new task data on the classification heads of old tasks consistent, we also employ KD to enforce the outputs after updating the old task models agree with the scores before the update; 2) to suppress the outputs of old task data on the classification heads of new tasks, their ground-truth target values are directly set to be zero for training.)
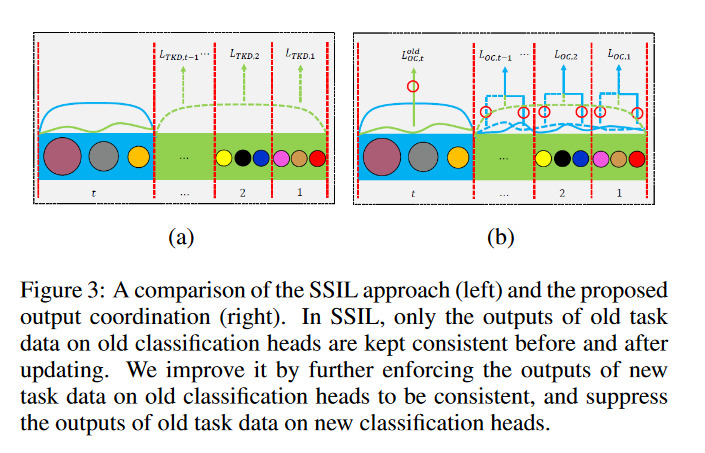
差异如图三所示:
3.3 输入协调
由于类别不平衡问题可能导致全连接层的学习权重出现重大偏差,因此输出分数$\hat{P}^{\tau}_{i,j}$可能和真实值$P^{\tau}_{i,j}$相差甚远,因此需要平衡权重
采用全连接层前一层的输出来调整权重:假设$\hat{q}^{\tau}_{i,j}$是输出分数前一层对应的向量,我们计算交叉熵$L_{ce,t}$对前一层向量的导数如下:(细节见目录)

这里存在的问题是,当某个样本的数据量很大的时候,模型会偏向于该类别,因此上面的公式会在学习过程中变得很小,为了去解决这个问题,我们提出了绝对值视为对应输入样本的权重加入到loss中,因此较小的泉州霓虹将自适应的分配给拥有更多输入数据的类别的样本,因此模型将更多的关注样本较少的类别
因此,我们利用绝对值$\delta_{i,j}^{\tau}$在训练期间为每个数据输入权重:
- 首先,我们利用输入梯度的绝对值合并到传统的交叉熵损失中:
$L_{IC,t}=-\frac{1}{N_{old}+n_{new} }\sum_{i,j,k=i,\tau=1}^ty^{\tau}_{i,j,k}\delta_{i,j,k}^{\tau}log(\hat{p}^{\tau}_{i,j,k})$ (7)
- 之后使用这个式子去平衡每一类的los,这样就能根据每个输入梯度的绝对值$\delta$来平衡全连接层的类别权重
它不仅缓解了增量学习中新旧任务之间的类别偏差,而且大大降低了任务内偏差


3.4 输出协调
更新旧任务模型之后,需要保持新任务数据$D^t$的输出分布一致;并且在新任务分类头上隐藏旧任务数据$D^t_{old}$。
In Figure 1, this is to keep the blue solid line consistent with the dotted line, and make the green solid line approach to 0
在训练第t个轮次的任务时,我们假设输出$D^t\cup D^t_{old}$的没有经过softmax层的分数由$\hat{z}^{\tau}_{i,j,k}$给出,并且在更新旧任务模型训练第k轮新任务时,输出的数据$D^t\cup D^t_{old}$分数是$\widetilde{z}^{\tau}_{i,j,k}$
通过考虑the principle of human inductive memory,使用KD知识蒸馏在更新对应模型前后,强制新任务数据在每个旧任务的分类头上的输出一致性
$L_{OC,1\rightarrow t-1}=\sum_{\tau=1}^{t-1}\left[\sum_{i,j,k}\rho_{KL}^{\epsilon}(\hat{z}^{\tau}_{i,j,k}-\widetilde{z}^{\tau}_{i,j,k})\right]$ (8)
$\rho_{KL}^{\epsilon}(·)$是蒸馏损失,$\epsilon$是缩放函数
旧任务数据在新类别头上的数据可以背调整,根据:
$L_{OC,t}^{old}=\frac{1}{n_{new}}\sum_{i,j,k}(\hat{p}^t_{i,j,k}-0)$,$i\in \{1,2,…,m(t-1)\}$
(8)的原理和SSIL相似,但是提出的输出协调机制和SSIL方法不同,结合一致损失$L_{IC,t}$(7),总体的输出损失为:
$L_{JIOC,t}=L_{IC,t}+\gamma_1 L_{OC,1\rightarrow t-1}+\gamma_2 L_{OC,t}^{old}$
其中$\gamma_1$和$\gamma_2$是两个权衡的超参数