最大子数组和乘积

[53] 最大子数组和

https://leetcode.cn/problems/maximum-subarray/description/

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]

输出：6解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

[152] 乘积最大子数组

https://leetcode.cn/problems/maximum-product-subarray/description/

给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续 子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

输入: nums = [2,3,-2,4]

输出: 6

解释: 子数组 [2,3] 有最大乘积 6。

METHOD-DP

我们先给出这两者的共通办法：DP，即动态规划

对于前者，求最大和，我们可以给出如下的转移方程：

DP表示的是当前下标的连续子数组最大和，因为DP只需要用到前面的DP[i-1]和当前数组nums[i]，因此我们在原数组上做DP即可

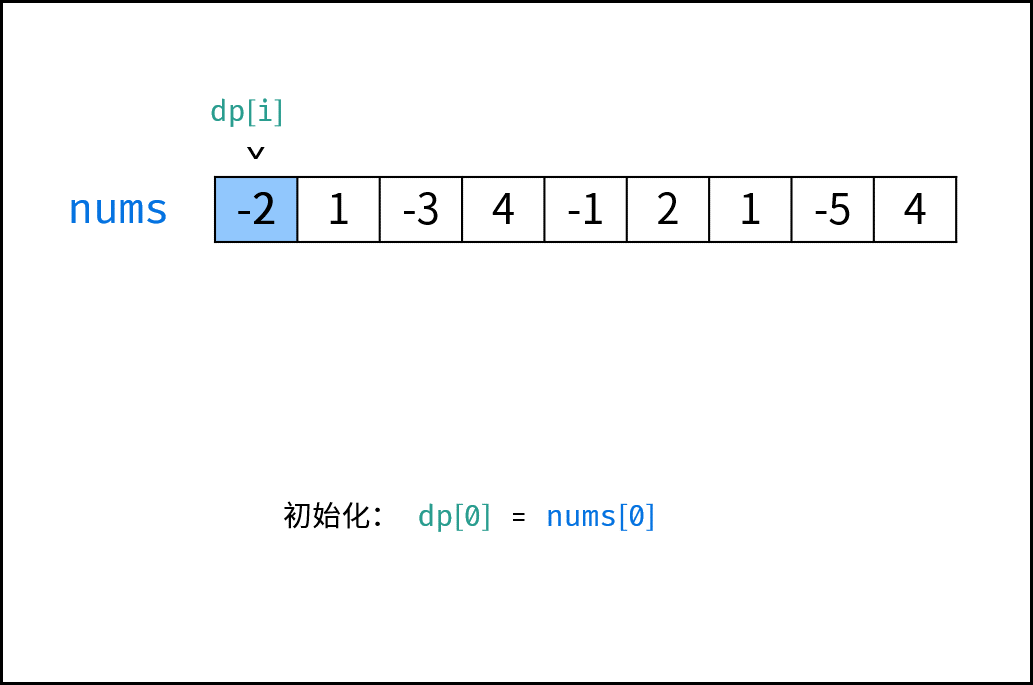
代码如下：

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        for i in range(1, len(nums)):
            nums[i] += max(nums[i-1], 0)
        return max(nums)

对于后者，其实实际上的转移方程类似：nums[i]前面的数之和为负数，则重新开始计算，为正数则继续计算。并且nums[i]的值是在nums[i-1]更新后计算出的，保证更新后 nums[i] 是以原来的nums[i]结尾的最大连续子数组和

但是这里我们需要做一个额外的考虑：由于存在负数，那么会导致最大的变最小的，最小的变最大的。因此我们在保存最大乘积的同时要保留最小乘积

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        if len(nums)==0:
            return None
        max_ans=1
        min_ans=1
        ans=nums[0]
        for i in range(len(nums)):
            #负值：max与min进行交换再进行下一步计算
            if nums[i]<0:
                max_ans,min_ans=min_ans,max_ans
            max_ans=max(max_ans*nums[i],nums[i])
            min_ans=min(min_ans*nums[i],nums[i])
            ans=max(max_ans,ans)
        return ans

METHOD-OTHERS

to be continued