[TOC]
1.key elements
即博弈论中的一些不可或缺的因素:PSPIR
- Players::$\geq 2$ (1个就变成规划了)
- Strategies:player做的一些决策
- Pay-Off:收益,即通过决策可以得到的东西(incentives)
- Information:知道什么
- Rationality:如何思考(是否理性)
实际上在实际中要考虑到道德等各方面的因素,无法做到完全理性,因此只能假设理性,这也是博弈论的缺陷所在
2.效益矩阵
| player(横2纵1) Strategy C | Strategy D | |
|---|---|---|
| Strategy A $P_{11}$ $P_{21}$ | $P_{12}$ $P_{22}$ | |
| Strategy B $P_{13}$ $P_{23}$ | $P_{14}$ $P_{24}$ |
- AB是Player1做出的策略;CD则是Player2做出的策略,P为收益,左边是1的收益矩阵,右侧则是2的收益矩阵
- $P_{ij}$指的是玩家i在情况j下的收益
效益矩阵实例化:囚徒困境
| player(横2纵1) Strategy C | Strategy D | |
|---|---|---|
| Strategy A -6 -6 | 0 -12 | |
| Strategy B -12 0 | -1 -1 |
- 这是囚徒困境的实例化,AC为坦白从宽,confess;BD表示抗阻从严
- 很明显:对Player1来说,无论2如何做,自己坦白从宽都是最佳策略;对2亦然如此
- 对他们来说,这个策略是纳什均衡的
- 纳什均衡:每个人理性上都不想改变自己的决策
- 一定存在
- 纳什均衡:每个人理性上都不想改变自己的决策
- 对他们来说,这个策略是纳什均衡的
- 全局视角下,很明显这不是最佳策略
- 理性:不选择严格劣的策略
- Each singal descison is not global optimum No-cooporativa,非合作下的决定不一定全局最优
- 囚徒困境只是特例,实际上AC\BD的策略并不一定相同
- 其他例子:
- Lesson for military
- Market Strategies
- Cooperation depend on morality, or the complicated dynamics of environment ?
| 田忌赛马(横田忌纵齐威王) | 上 | 中 | 下 |
|---|---|---|---|
| 上 | 1 -1 | 1 -1 | 1 -1 |
| 中 | -1 1 | 1 -1 | 1 -1 |
| 下 | -1 1 | -1 1 | 1 -1 |
- 田忌能赢的原因:信息不对等
3.Person Game:Simple Sum
- RULE:一堆金币,有两个人彼此博弈,每个人每次能拿k枚,轮换拿,拿到最后那枚金币的获胜
- Lemma:当每人能拿k枚硬币的时候,能够拿完硬币剩下i(k+1)(i\k为非负整数)的人获胜
- Proof:
- i=1时候显然成立(无论先手拿完多少后手都可以全部拿走而获胜,而且先手不可能全部拿完)
- 假设i=N的时候成立
- 那么i=N+1的时,总共有(N+1)(k+1)枚硬币,这时候假设先手拿t枚硬币,那么后手拿k+1-t枚硬币即可回到ii的状态,因此后手(剩下i(k+1))一定获胜
- Proof:
- 因此对于上面这个结果,先手的人在金币数除以k+1取模剩余1~k的时候都必胜,后手只在为k+1的时候必胜
- 这是一个序列博弈:Sequential Game Theory
4.五个海盗分金币
RULE:5个海盗偷到1000枚金币,怎么分?、
- 按照A>B>C>D>E的方式进行分配,第一位海盗进行分配方案确定,加上自己共有半数同意即可通过分配方案;如果没有通过,则被杀死,换第二个进行分配;… 依次类推
- 如果你是A,该怎么提方案?
条件:理性的人在相同情况下倾向于让游戏后结束-边界条件
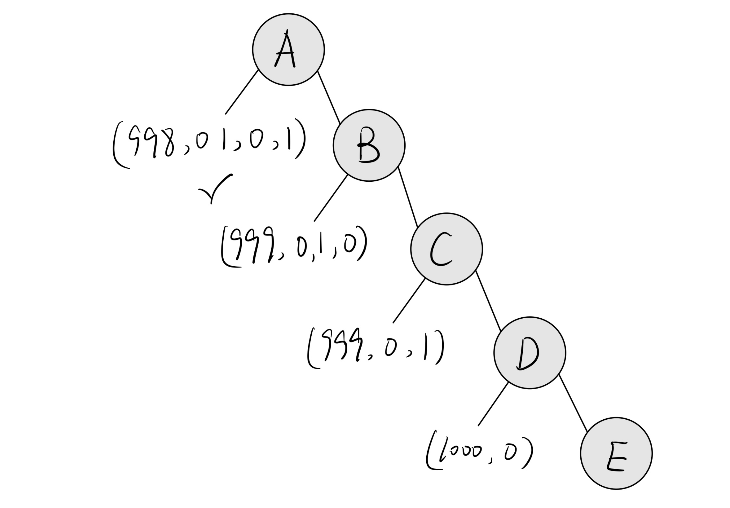
- 采用树的形式,从尾部开始考虑:
- 对D:(1000,0),因为自己能保证通过
- 对C:(999,0,1),这样能让E通过,因为E如果不同意后面就一块拿不到
- 对B:(999,0,1,0),这样能让D通过,刚好两票,原因同上
- 对A:(998,0,1,0,1),,这样能让BD通过,原因同上
5.一些博弈类型分类
(1) 合作博弈与非合作博弈
- 前者彼此不能通信,后者能有协定
囚徒困境就是非合作博弈,如果串供就是合作博弈
(2)零和博弈:总收益为0
石头剪刀布
Battle of sexes 性别战:非零和博弈
(3)瞬时和序列博弈
- 后者一般采用树的动态过程,类似海盗类型题
(4)完美和不完美信息博弈
- 后者不知道对方的决策
- 完美博弈不等于完全博弈
- 完美是知道对方的决策(如下围棋),而完全是知道对方的收益矩阵
最后通牒博弈:序列、完美博弈
打牌是不完美信息博弈