[TOC]
1.1 策略式博弈
Strategy game = Normal Form Game
full information(完全信息)+ non-cooperate(非合作)+ simultaneously(同时)
定义:
N players
For each players $i\in [1,N]$ , $A_i$ (一个动作集)
$u_i, A_1\times A_2 \times A_3\times …\times A_n\rightarrow R,i\in N$
or a preference relation $\succeq_i $ over A for $i \in N$
(推广策略式博弈到:偏好)
outcome:$a=(a_1,a_2,a_3,…,a_2)$
收益函数 $u_i$ 可以被偏好关系替代:$≳$
A perference(偏好关系)$≳$ over a set A satisfies:
完备性 complete
$a\succeq b$ or $b\succ a$ for every $a\in A,b \in A$
反身性 reflexive
$a ≳ a$ for every a$\in $A
传递性 transitive
if $a≳b$ , $b≳c$,than $a≳c$ for every a , b , c $\in$A
举例:囚徒困境
- N={1,2}
- $A_1=A_2=\{Confess,Don’t Confess\}=\{C,D\}$
- $(C,C)_1$=-6 ; $(C,C)_2=-6$ ; $(C,D)_1=-1$ ; $(C,D)_2$=-12 ; …
A Game :
$G=\{N,\{A_i\}_{i=1}^N,\{u_i\}_{i=1}^N\}$
$G=\{N,\{A_i\}_{i=1}^N,\{\succeq\}_{i=1}^N\}$
$A_{-i}$:
除了Player i之外的所有人的 outcome/action :
$A_{-i}=A_1\times A_2\times …\times A_{i-1}\times A_{i+1}\times …A_n$
1.2 纳什均衡 Nash Equilibrium (NE)
$a^=(a_1^,a_2^,…,a_n^)$ is a NE if for $\forall$ Player i $u_i^(a_i^,a_{-i}^)\geq u_i(a_i,a_{-i}^)$ for all $a_i \in A_i$
即对任何人来说,在其他人的选择条件不变时,当前选择最佳
- 对任何人调整策略收益都不会增加
- self-enforcing : no player has an encentive to alter his strategy intentively
| player(横2纵1) | Confess | Don’t Confess |
|---|---|---|
| Confesss | -6 -6 | 0 -12 |
| Don’t Confess | -12 0 | -1 -1 |
- NE:(C,C)
1.4.1 Best Response Correspondence
$B_i(A_{-i})=\{a_i \in A_i,u_i(a_i,a_{-i})\succeq u_i(b_i,a_{-i}),\forall b_i \in A_i\}$
$B_1(C)=C$ : 第一个人的在其他人行动条为confess时的最大利益回应
类似的:$B_1(D)=C$ ;$B_2(C)=C$;$B_2(D)=C$
1.4.2
假设$(q_1^,q_2^)$ 是一个纳什均衡策略
player i makes the best strategies $q_i^ $ with respect to $ q^_{-i} $
1.4.3 one way of finding Nash eqilibria for payoff matrix
Find the best response correspondence for each player
best response correspondence gives the set of payoff maximizing strategies for each strategy profile of the other players
Find where they intersect
Find all outcomes $(a_1^,a_2^,…,a^_N)$ such that $a_i^\in B_i(a^*_{-i})$
1.4.4 Primitive hunting
| player(横2纵1) r | B |
|---|---|
| Rabbit(r) 3 3 | 3 0 |
| Bear(b) 0 3 | 9 9 |
$B_1(r)=\{r\}$ ; $B_1(b)=\{b\}$ ; $B_2(r)=\{r\}$ ; $B_2(b)=\{b\}$
考虑$(a_1^,a_2^$) 满足 $a_1^ \in B_1(a_2^) $ and $a_2^ \in B_2 (a_1^)$ 这时候构成纳什均衡
纳什均衡点:$(r,r)$,$(b,b)$
1.4.5 Rock-Paper-Scissors 石头剪刀布
纯策略博弈可能没有纳什均衡点,但是概率性的混合事件有纳什均衡,因此还是一定存在纳什均衡
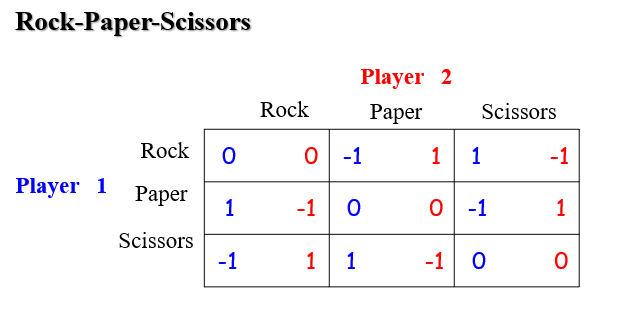
- exercise:
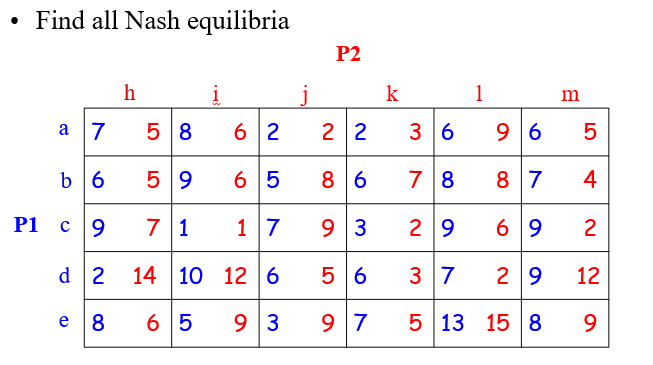
1.4.6 例
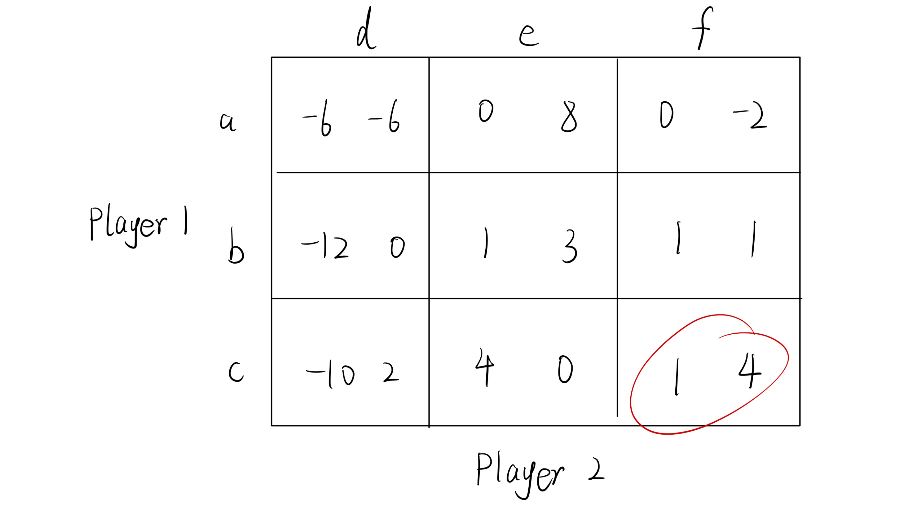
$a_2^=d$ 的时候,$a_1^=a$,此时不满足
$a_2^=e$的时候,$a_1^=c$,此时不满足
…
- (c,f) 为唯一纳什均衡点
1.4.7 例3
$G=\{\{1,2,3\},\{\{a,b,c\},\{x,y,z\},\{L,R\}\},\{u_i\}_{i=1}^3\}$
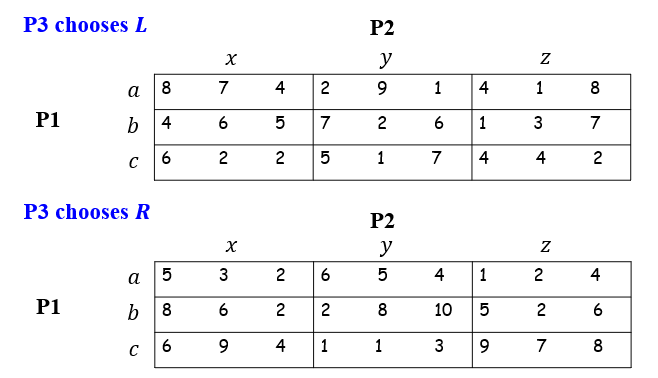
考虑:(a,x,L)=(8,7,4):不是
考虑:(a,y,R)=(6,5,4): 是
- $a\in B_1(y,R)$
- $y\in B_2(a,R)$
- $R\in B_3(a,y)$
1.5 如何寻找连续策略的纳什均衡
One way of finding Nash equilibrium for continuous strategies $A_i$
Find the best response correspondence for each player
Best response correspondence:
$B_i(a_{-i})=\{a_i argmax_{a_i\in A_i}u_i(a_i,a_{-i}) \}$
Find all Nash Equilibria ($a_1^,a_2^,…,a_N^$) such that $a_i^ B_i(a_{-i}^*)$ for each player
1.5.1 古诺竞争
说明:两家公司竞争要选择生产多少产品
$G=\{ \{1,2\},\{q_1,q_2\},\{\mu_1,\mu_2\} \}$
Price:$p(q_1+q_2)=max(0,a-b(q_1+q_2))$
- Costs(i=1,2):$c_i(q_i)=cq_i$
- Payoffs(i=1,2):$\mu_i(q_1,q_2)=(max(0,a-b(q_1+q_2))-c)q_i$
- Condition:$a>0,c>0,q_1\geq0,q_2\geq 0$
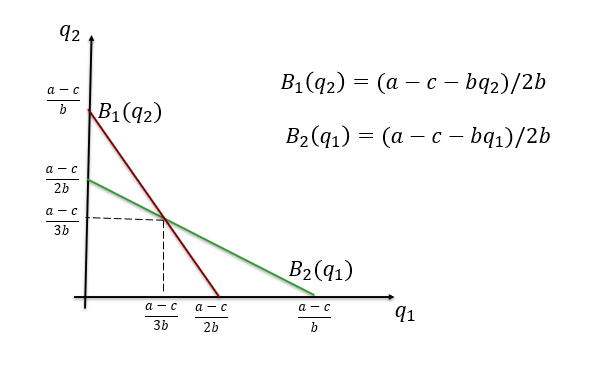
best response correspondence: $B_i(q_{-i})=max(0,(a-c-bq_{-i})/2b)$
Proof:
如果$q_2\geq \frac{a-c}{b}$ ,$\mu_2(q_1,q_2)\leq0$, $q_1=0$,$B_1(q_2)=0$
如果$q_2< \frac{a-c}{b}$,$\mu_i(q_1,q_2)=(a-c-b(q_1+q_2))q_i$
$\frac{\partial \mu_1}{\partial q_1}=a-c-bq_2-2bq_1=0$
$q_1=(a-c-bq_{2})/2b$
NE:
Proof:
Prove $q_1^>0,\quad q_2^>0$ by contradiction
$q_1^>0,q_2^>0$:
$q_1^=B_1(q_2^)=(a-c-bq_{2}^*)/2b$
$q_2^=B_1(q_1^)=(a-c-bq_{1}^*)/2b$
1.5.2 伯特兰德模型 Bertrand Model
两个公司公开招标报价:
市场交易价格是最低的报价:$min\{q_1,q_2\}$
每个公司给一个报价策略$q_1$和$q_2$
Output demand:$d=a-min(q_1,q_2)$
Cost:$C_i(q_i)=cq_i$(a>c)
Payoff:
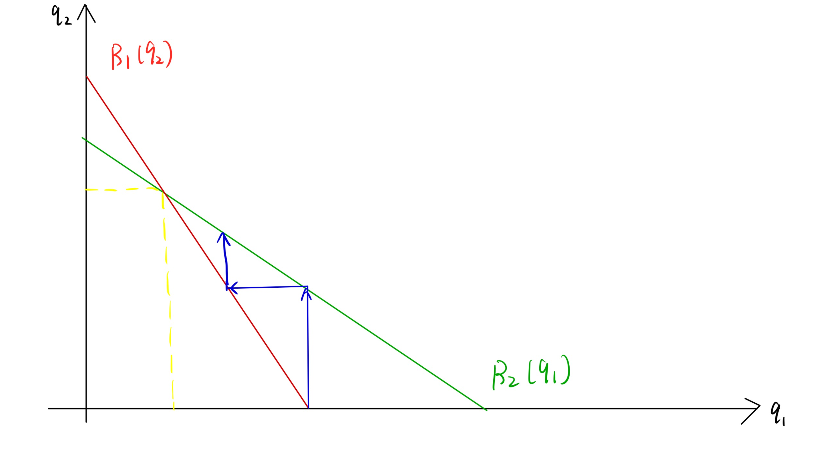
那么$B_1$的最佳回复$B_1(q_2)$为:
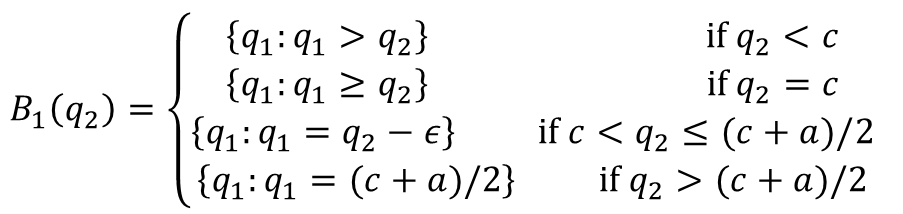
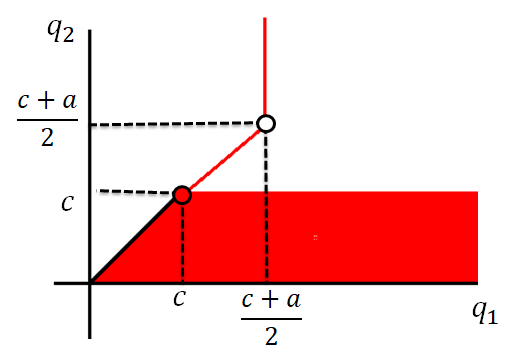
纳什均衡策略$(q_1^,q_2^)$需要满足$q^_1\in B_1(q_2^)$,$q^_2\in B_2(q_1^)$
Intersection of the graphs of the best response function
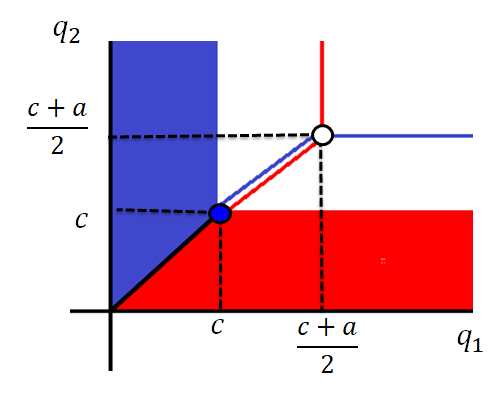
- NE:(c,c)
1.6 选择 Election
- Several candidates vote for political office
- Each candidate chooses a policy position
- Each citizen, who has preferences over policy positions, votes for one of the candidates
- Candidate who obtains the most votes wins
Strategic game:
- Players: candidates
- Set of actions of each candidate: set of possible positions
- Payoff is 1 for winner; is 0.5 for ties; and is 0 for loser
- Note: Citizens are not players in this game
1.6.1 Example 1
Two candidates $N=\{1,2\}$
Set of possible position: $b_1,b_2 \in [0,1]$
•Citizens are continuous, and are distributed uniformly on [0,1], and vote for the candidate with closet position
Payoff:
$B_i(b_j)$:
- $b_j<\frac{1}{2}$:$B_i(b_j)=\{b_i:b_j<b_i<1-b_j\}$
- $b_j=\frac{1}{2}$:$B_i(b_j)=\{b_i:b_i=\frac{1}{2}\}$
- $b_j>\frac{1}{2}$:$B_i(b_j)=\{b_i:1-b_j<b_i<b_j\}$

- NE:$(\frac{1}{2},\frac{1}{2})$
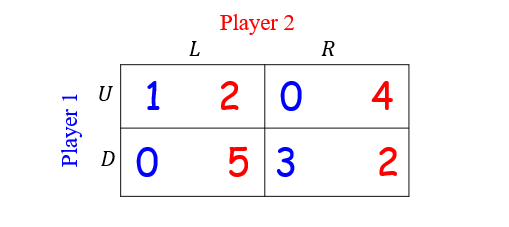
1.7.1 Example 2
- $G=\{\{1,2\},\{\{U,L\},\{L,R\}\},\{u_1,u_2\}\}$