第二章 混合式博弈和纳什策略

[TOC]

2.1 Mixed Strategy

2.1.1 引入：选举 Election（Hotelling-Downs 模型）

Several candidates vote for political office

Each candidate chooses a policy position

Each citizen, who has preferences over policy positions, votes for one of the candidates

Candidate who obtains the most votes wins

Strategic game:

• Players: candidates

• Set of actions of each candidate: set of possible positions

• Payoff is 1 for winner; is 0.5 for ties; and is 0 for loser

Note: Citizens are not players in this game

Two candidates N={1,2}

Set of possible position: $b_1, b_2∈[0,1]$

Citizens are continuous, and are distributed uniformly on [0,1], and vote for the candidate with closet position.

Payoff：$u_i(b_1, b_2) = \begin{cases} 1 & \text{if } i \text{ wins} \\ 0.5 & \text{if } i \text{ ties} \\ 0 & \text{if } i \text{ loses} \end{cases}$

每个候选人将从一组可选的政策立场中选择一个概率分布。

• 候选人会选择一个策略，使得在考虑到其他候选人选择的政策时，自己的预期支付最大化。
• 混合策略可能是一个概率分布，表示每个候选人按照这个分布选择一个政策位置
• 混合策略实际上会导致候选人在某种程度上模糊化他们的政策立场，以便最大化他们吸引中间选民的机会，同时确保不被其他候选人超越

对$B_i(b_j)$：

$$\begin{align} &\text{If } b_j < \frac{1}{2}, \quad B_i(b_j) = \{ b_i : b_j < b_i < 1 - b_j \}\\ &\text{If } b_j = \frac{1}{2}, \quad B_i(b_j) = \{ b_i : b_i = \frac{1}{2} \}\\ &\text{If } b_j > \frac{1}{2}, \quad B_i(b_j) = \{ b_i : 1 - b_j < b_i < b_j \}\\ \end{align}$$

1. 候选人1和候选人2的目标是最大化自己获得的选票。每个选民会选择距离自己最近的候选人投票。如果两个候选人选择的位置不同，那么选民会选择距离自己最近的一个候选人。

2. 假设选民位于某个位置 $x \in [0, 1]$，如果 $x < \frac{b_1 + b_2}{2}$，则选民会选择候选人1；如果 $x > \frac{b_1 + b_2}{2}$，则选民会选择候选人2。这个临界点是 $x = \frac{b_1 + b_2}{2}$，表示两个候选人选民投票的“分界线”

   1. 这很容易理解，当我们选择$B_i$最佳回应时候，让x为$b_i$与临界线做相应的比较比克

3. 候选人趋向于选择中间位置，即 $b_1$ 和 $b_2 $会收敛到相同的位置，即 $b_1 = b_2 = 0.5$。这种行为可以解释为候选人会试图吸引中间选民，因此趋向于选择政策谱系的中点。

4. 当两个候选人选择相同的位置时，他们会吸引同样的选民，因此会形成平局，每个候选人获得0.5的支付。
5. 如果其中一个候选人偏离了中点，另一个候选人将会吸引更多选民，最终导致偏离中点的候选人失去选举。因此，选择中间位置是双方的最优策略，这就是这次博弈中的纳什均衡

2.1.2 defination混合策略定义

Mixed strategy keeps the guess of player’s strategies, keep unpredictable on pure strategies

Pure strategy can be viewed as a special mixed strategy：

$G = \{ N, \{ A_1, A_2, \dots, A_N \}, \{ u_1, u_2, \dots, u_N \} \}$

Pure strategy: strategies set of player $i$$：A_i = \{ a_{i1}, a_{i2}, \dots, a_{i n_i} \}$

Mixed strategy: a probability over the set $A_i$ of strategies

$A_i = \{ a_{i1}, a_{i2}, \dots, a_{i n_i} \}$

$p_i = (p_{i1}, p_{i2}, \dots, p_{i n_i})$

• 即有$p_{ij}$概率的选择$a_{ij}$，对每一个player在每一个action上有一个概率

Denote by $\Delta(A_i)$ the set of all probability distributions over $A_i$

$\Delta(A_i) = \{ p_i = (p_{i1}, p_{i2}, \dots, p_{i n_i}) : p_{ij} \geq 0, \sum_j p_{ij} = 1 \}$

$\Delta(A_i)$ 通常表示玩家 $i$ 的 混合策略空间。是一个包含所有可能混合策略的集合，其中每个混合策略是一个概率分布，指定了玩家选择不同动作的概率。

$\Delta(A_i) = \{ p_i = (p_{i1}, p_{i2}) : p_{i1} \geq 0, p_{i2} \geq 0, p_{i1} + p_{i2} = 1 \}$

• 玩家 $i$ 的动作集合 $A_i = \{a_1, a_2\}$，即玩家可以选择动作 $a_1$ 或者动作 $a_2$

• 选择混合策略，例如 $p_{i1} = 0.7$ 和 $p_{i2} = 0.3$，这表示玩家以70%的概率选择 $a_1$，以30%的概率选择 $a_2$。

• $\Delta(A_i)$表示了第$i$个玩家可选的概率操作$(p_1,p_2,…)$

2.1.3 混合策略例子

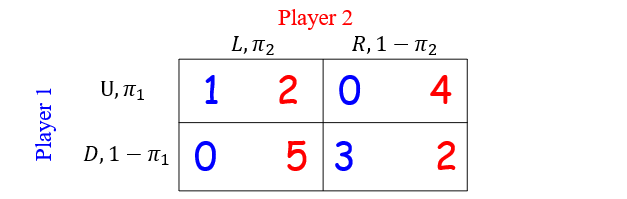
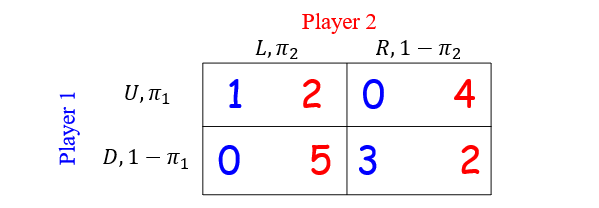
$p = (p_1, p_2) = \left( (0.4, 0.6), (0.5, 0.5) \right)$

$U_1(p) = p_1(U) p_2(L) u_1(U, L) + p_1(U) p_2(R) u_1(U, R) $

$+ p_1(D) p_2(L) u_1(D, L) + p_1(D) p_2(D) u_1(D, R) = 1.1$

$U_2(p) = \dots = 3.3$

1. U：$U_i(p)$ 通常表示玩家 $i$ 在给定策略概率分布 $p$ 下的期望效用
2. u₁(U, L)：表示玩家1的效用函数，即玩家1在特定策略组合下的收益。具体来说，u₁(U, L) 是当玩家1选择策略 U（上），且玩家2选择策略 L（左）时，玩家1的效用或收益。

• $p_1(U)$ 是玩家1选择策略 U（上）的概率。
• $p_1(D)$ 是玩家1选择策略 D（下）的概率。
• $p_2(L)$ 是玩家2选择策略 L（左）的概率。
• $p_2(R)$ 是玩家2选择策略 R（右）的概率。
• $u_1(U, L)$ 是玩家1在策略组合 (U, L) 下的效用。
• $u_1(U, R)$ 是玩家1在策略组合 (U, R) 下的效用。
• $u_1(D, L)$ 是玩家1在策略组合 (D, L) 下的效用。
• $u_1(D, R)$ 是玩家1在策略组合 (D, R) 下的效用。

Given $G = \{ N, \{ A_i \}, \{ u_i \} \}$ and mixed $p = (p_1, p_2, \dots, p_N)$, the expected payoff of player $i$ is given by

$U_i(p) = \sum_{a \in A} p(a) u_i(a) \\= \sum_{a = (a_1, \dots, a_N) \in A} p_1(a_1) \times \dots \times p_N(a_N) u_i(a)$

Pure strategy game:$G = \{ N, \{ A_1, A_2, \dots, A_N \}, \{ u_1, u_2, \dots, u_N \} \}$

Mixed strategy game:$G = \{ N, \{ \Delta(A_1), \Delta(A_2), \dots, \Delta(A_N) \}, \{ U_1, U_2, \dots, U_N \} \}$

2.2 Lemma

2.2.1 Lemma 1

$U_i(p)$ is a continuous function for each variable.(如果玩家 i 的混合策略 p中的某个概率发生变化（即某个策略的选择概率发生变化），那么玩家 i 的期望效用 $U_i(p)$ 也会发生连续变化，不会出现突变或不连续的情况。)

Proof:

$U_i(p) = \sum_{a = (a_1, \dots, a_N) \in A} p_1(a_1) \times \dots \times p_N(a_N) u_i(a)$

对于每种可能的策略组合 $a = (a_1, a_2, \dots, a_N)$，其概率为 $p_1(a_1) \times p_2(a_2) \times \dots \times p_N(a_N)$，而 $u_i(a)$ 是给定策略组合 a 时玩家 i 的效用。通过对所有可能的策略组合加权平均，我们就得到了玩家 i的期望效用 $U_i(p)$

Given $p = (p_1, p_2, \dots, p_N)$, we write $U_i(a_j, p_{-j}) = \sum_{a_{-j} \in A_{-j}} p_{-j}(a_{-j}) u_i(a_j, a_{-j})$

这个式子表示，对于某个玩家 i的action $a_j$的期望效用$U_i(a_j, p_{-j}) $是所有其他玩家 j 的策略 $a_{-j} $和其他玩家的策略 $ u_i(a_j, a_{-j})$ 下的加权效用,$a_{-j} \in A_{-j}$可能有很多种概率的组合形式

Then $U_i(p) = \sum_{a_j \in A_j} p_j(a_j) U_i(p_{-j}, a_j)$

玩家 i 的总期望效用是通过玩家 j 的策略 $a_j $来加权每个条件期望效用$U_i(p_{-j}, a_j)$ 得到的，因此期望效用会根据每个玩家的$p_j(a_j)$变化

2.2.2 Lemma 2

The expected payoff function $U_i$ is multi-linear.(线性性)

For mixed outcomes $p = (p_1, p_2, \dots, p_N)$ and $p_j’$, we have:

$$U_i(\lambda p_j + (1 - \lambda) p_j', p_{(-j)}) = \lambda U_i(p_j, p_{(-j)}) + (1 - \lambda) U_i(p_j', p_{(-j)}), \\ \lambda \in [0,1]$$

证明过程如下：

我们首先回顾期望效用函数的定义，它是每个可能策略组合的概率和效用的加权平均：

$U_i(p) = \sum_{a_j \in A_j} p_j(a_j) U_i(p_{(-j)}, a_j)$

其中 $p_j(a_j) $是玩家 j 选择策略$a_j$ 的概率，而$U_i(p_{-j}, a_j)$ 是当玩家 j 选择策略 $a_j$ 时，其他玩家的策略为$p_{-j}$ 时玩家 i 的期望效用。

现在，我们考虑两种混合策略 $p_j $和$p_j’$，新的混合策略是由这两种策略的线性组合构成：

$\tilde{p_j} = \lambda p_j + (1 - \lambda) p_j’.$

玩家 i 在这种新的混合策略下的期望效用可以写作：

$U_i(\tilde{p_j}, p_{-j}) = U_i(\lambda p_j + (1 - \lambda) p_j’, p_{-j})$

我们根据期望效用函数的定义，可以将其展开：

$U_i(\lambda p_j + (1 - \lambda) p_j’, p_{-j}) = \sum_{a_j \in A_j} \tilde{p_j}(a_j) U_i(p_{-j}, a_j)$

由于$\tilde{p_j}(a_j) = \lambda p_j(a_j) + (1 - \lambda) p_j’(a_j)$，我们将其代入：

$U_i(\lambda p_j + (1 - \lambda) p_j’, p_{-j}) \\= \sum_{a_j \in A_j} \left( \lambda p_j(a_j) + (1 - \lambda) p_j’(a_j) \right) U_i(p_{-j}, a_j)$

据加法的线性性质，展开后我们得到：

$$U_i(\lambda p_j + (1 - \lambda) p_j', p_{(-j)}) \\= \lambda \sum_{a_j \in A_j} p_j(a_j) U_i(p_{(-j)}, a_j) + (1 - \lambda) \sum_{a_j \in A_j} p_j'(a_j) U_i(p_{(-j)}, a_j).$$

这正是：

$\lambda U_i(p_j, p_{(-j)}) + (1 - \lambda) U_i(p_j’, p_{(-j)})$

因此证明了期望效用函数 $U_i $的线性性质，即它是多线性的（multi-linear）。

2.3 Mixed Strategy Nash Equilibrium

An mixed strategy outcome $p = (p_1, p_2, \dots, p_N)$ is a Nash equilibrium (NE) if for each $i$, we have

$$U_i(p_i, p_{(-i)}) \geq U_i(p_i', p_{(-i)}), \quad \text{for } p_i' \in \Delta(A_i)$$

• $U_i(p_i, p_{(-i)})$：表示玩家 $i$ 在给定混合策略 $p_i$ 和其他所有玩家的混合策略 $p_{(-i)}$ 下的效用（即玩家 $i$ 的期望收益）。其中，$p_i$ 是玩家 $i$ 选择的混合策略，$p_{(-i)}$ 是除玩家 $i$ 外所有其他玩家的混合策略。
• $p_i’$：表示玩家 $i$ 可能选择的任何一个替代混合策略。
• $\Delta(A_i)$：表示玩家 $i$ 的策略集合（$A_i$）上的所有可能的混合策略，即玩家 $i$ 选择某一动作的概率分布。
• $U_i(p_i’, p_{(-i)})$：表示玩家 $i$ 在选择替代混合策略 $p_i’$ 时的效用，即当玩家 $i$ 改变策略为 $p_i’$，而其他玩家保持不变时，玩家 $i$ 的期望收益。

如果玩家 $i$ 选择了一个混合策略 $p_i$，而其他玩家的策略是 $p_{-i}$，那么玩家 $i$ 的期望效用应该是最大化的。如果玩家 $i$ 能通过改变自己的混合策略 $p_i’$ 来获得更高的收益，那么 $p$ 就不是一个纳什均衡。因此，纳什均衡的定义要求对于每个玩家 $i$，无论他选择什么样的混合策略，给定其他玩家的策略，他都无法通过单方面改变自己的策略来获得更大的期望效用。

• 假设有一个两人博弈，其中每个玩家都有两个动作，分别是 上（U） 和 下（D）。我们考虑玩家1和玩家2的混合策略：

  • 玩家1的混合策略为 $p_1 = (p_1(U), p_1(D))$，即玩家1选择“上”动作的概率为 $p_1(U)$，选择“下”动作的概率为 $p_1(D)$。

  • 玩家2的混合策略为 $p_2 = (p_2(L), p_2(R))$，即玩家2选择“左”动作的概率为 $p_2(L)$，选择“右”动作的概率为 $p_2(R)$。

  • 如果这个策略组合 $p = (p_1, p_2)$ 是一个混合策略纳什均衡，那么对于每个玩家 $i$（无论是玩家1还是玩家2），在其他玩家的策略保持不变的情况下，他不能通过改变自己的混合策略来增加自己的期望收益。

例如，玩家1的期望效用为：

$U_1(p_1, p_2) = p_1(U) \cdot U_1(U, L) + p_1(D) \cdot U_1(D, L)+p1(U)⋅U1(U,R)+p1(D)⋅U1(D,R)+ p_1(U) \cdot U_1(U, R) + p_1(D) \cdot U_1(D, R)$

而如果玩家1选择了某个替代策略 $p_1’$，则他的期望效用为：

$U_1(p_1’, p_2) = p_1’(U) \cdot U_1(U, L) + p_1’(D) \cdot U_1(D, L)+p1′(U)⋅U1(U,R)+p1′(D)⋅U1(D,R)+ p_1’(U) \cdot U_1(U, R) + p_1’(D) \cdot U_1(D, R)$

根据纳什均衡的定义，玩家1的期望效用 不应该低于 选择当前混合策略 $p_1$ 时的效用，即：

$U_1(p_1, p_2) \geq U_1(p_1’, p_2)$

同样的条件也适用于玩家2的策略。只有在这种情况下，$p = (p_1, p_2)$ 才是一个混合策略纳什均衡。

Given $G = \{N, \{\Delta(A_i)\}, \{U_i\}\}$ and $p = (p_1, \dots, p_N)$, the best response correspondence of player $i$ is given by

$$B_i(p_{(-i)}) = \{ p_i : U(p_i, p_{(-i)}) \geq U(p_i', p_{(-i)}) \text{ for all } p_i' \in \Delta(A_i) \}$$

• 最优响应是一个玩家在知道其他玩家策略的情况下，选择能带来最大效用的策略集合。简单来说，对于给定的其他玩家的策略组合$p_{-i}$，最优响应就是玩家 $i$ 在这些策略下能选择的最好的混合策略。
• $B_i(p_{-i})$ 是玩家 $i$ 的最优策略集合，它包含了所有能够使得玩家 $i$ 获得最大效用的策略。就是说，玩家 $i$ 在选择混合策略时，会选择一个策略 $p_i$，使得玩家 $i$ 的效用最大化，而且不可能有其他策略能提供更高的效用。
• 假设有一个博弈，玩家 $i$ 只能选择两种策略：$A_1$ 和 $A_2$。其他玩家的策略是 $p_{-i} = (p_2, p_3)$。玩家 $i$ 的效用函数是 $U_i$，那么：
  • 玩家 $i$ 会选择混合策略 $p_i = (p_1, 1 - p_1)$，使得其期望效用最大化。
  • 对于所有可能的策略 $p_i’$，玩家 $i$ 会选择使得 $U_i(p_i, p_{-i}) \geq U_i(p_i’, p_{-i})$ 的那个策略 $p_i$。

Theorem: A mixed outcome $p = (p_1, \dots, p_N)$ is a NE if and only if $p_i \in B_i(p_{(-i)})$

Theorem: Every finite strategic game has a mixed strategy Nash equilibrium

• finite players
• each player has finite pure strategies
• Why is this important
  • Difficult to understand properties (NE) without existence
  • Find the NE if we know the existence of NE

2.3.1 An Property of MNE

Theorem If a mixed strategy is a best response, then each of the pure strategies (positive prob.) involved in the mixed strategy must be a best response. Particularly, each must yield the same expected payoff.(如果一个混合策略是一个最优反应（best response），那么在该混合策略中出现的每一个纯策略（即具有正概率的策略）必须也是最优反应，并且它们的期望效用必须相同)

If a mixed strategy $p_i$ is a best response to the strategies of the others $p_{-i}$, then each pure strategy $a_j s.t. p_i (a_j) > 0 $ is itself a best response to $p_{-i}$.

Particularly, all $U_i (a_j,p_(-i))$ must be equal

• 前半部分：假设玩家选择一个混合策略，并且这个混合策略是最优反应。那么，混合策略中每个正概率的纯策略（被玩家实际选择的策略）也必须是最优反应。这意味着，如果混合策略中有某个纯策略，且它有正的概率被选择，那么在该纯策略下，该玩家的期望效用应该是最大化的。
• 后半部分：这些正概率的纯策略必须使玩家的期望效用相同。换句话说，如果玩家在混合策略中选择多个纯策略，那么这些策略的期望效用必须是一样的，因为混合策略的期望效用是基于这些纯策略的加权平均值。如果一个策略的期望效用比其他策略高，玩家会倾向于选择这个策略，而不可能同时使用其他纯策略。

Theorem $G={N, {A_i }, {u_i}}, p=(p_1,p_2,…, p_N)$ is a mixed Nash equilibrium if and only if every pure strategy of player i with positive probability is a best response to $p_{-i}$

如果在博弈 $G = \{N, {A_i}, {u_i}\}$ 中，混合策略 $p = (p_1, p_2, \dots, p_N)$ 是一个纳什均衡（Nash Equilibrium），那么对于每个玩家 $i$，所有在混合策略中具有正概率的纯策略都是对其他玩家策略 $p_{-i}$ 的最佳反应（best response）；反之，如果每个在混合策略中具有正概率的纯策略都是最佳反应，那么该混合策略是纳什均衡。

充分性证明：

假设在混合策略 $p = (p_1, p_2, \dots, p_N)$ 下，对于每个玩家 $i$，所有在混合策略中具有正概率的纯策略 $a_j$ 都是对 $p_{-i}$ 的最佳反应。即对于玩家 $i$ 的所有正概率纯策略 $a_j$，都有：

$$U_i(a_j, p_{-i}) \geq U_i(a_j', p_{-i}) \quad \forall a_j' \in A_i$$

我们需要证明 $p$ 是一个混合纳什均衡。

1. 对于玩家 $i$ 来说，混合策略 $p_i$ 是给定其他玩家策略 $p_{-i}$ 时能够最大化其期望效用的策略。如果每个正概率的纯策略 $a_j$ 对 $p_{-i}$ 都是最佳反应，那么它们的期望效用相同，因此玩家 $i$ 不会倾向于通过单独改变策略来获得更好的效用。

2. 玩家 $i$ 的期望效用是：

   $U_i(p) = \sum_{a_j \in A_i} p_i(a_j) U_i(a_j, p_{-i})$

3. 由于每个正概率的纯策略 $a_j$ 都是最佳反应，所以对于所有选择的纯策略 $a_j$，它们的效用 $U_i(a_j, p_{-i})$ 是相同的。因此，混合策略 $p_i$ 在所有正概率的纯策略上提供相同的效用，因此没有玩家能够通过单独改变策略来提高期望效用，从而 $p$ 是纳什均衡。

必要性证明：

假设 $p = (p_1, p_2, \dots, p_N)$ 是一个混合纳什均衡，我们需要证明对于每个玩家 $i$，在混合策略中具有正概率的纯策略都是对 $p_{-i}$ 的最佳反应。

1. 由于 $p$ 是纳什均衡，意味着对于任意玩家 $i$ 和其混合策略 $p_i$，给定其他玩家的策略 $p_{-i}$，玩家 $i$ 的期望效用已经最大化。

2. 如果玩家 $i$ 在混合策略 $p_i$ 中选择纯策略 $a_j$，且 $p_i(a_j) > 0$，那么玩家 $i$ 在选择该策略时，其期望效用为：

   $$U_i(a_j, p_{-i}) \geq U_i(a_j', p_{-i}) \quad \forall a_j' \in A_i$$

3. 因此，玩家 $i$ 选择纯策略 $a_j$ 时的期望效用 $U_i(a_j, p_{-i})$ 必须不小于选择任何其他纯策略 $a_j’$ 的期望效用。这说明，在混合策略中具有正概率的纯策略 $a_j$ 都是最佳反应。

2.3.2 例子1

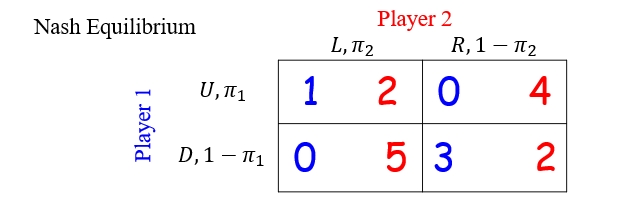
Fixed Player 1, the expectation payoff of Player 2 on L:$2\pi_1+5(1-\pi_1)$

the expectation payoff of Player 2 on R:$4\pi_1+2(1-\pi_1)$

Nash Equilibrium implies :$2\pi_1+5(1-\pi_1)=4\pi_1+2(1-\pi_1)→π_1=3/5$ (否则就会偏向于其中一个选择LorR，不会是混合式的)

Fixed Player 2, the expectation payoff of Player 1 on U：$\pi_2$

the expectation payoff of Player 1 on D:$3(1-π_2)$

Nash Equilibrium implies $π_2=3(1-π_2 )→π_2=3/4$

Nash Equilibrium:
Player 1 selects the mixed strategy $p_1 = \left( \frac{3}{5}, \frac{2}{5} \right)$ over ${U, D}$.
Player 2 selects the mixed strategy $p_2 = \left( \frac{3}{4}, \frac{1}{4} \right)$ over ${L, R}$.

The expected payoff of Player 1 on mixed strategy $p = (p_1, p_2)$:

$$\frac{3}{5} \times \frac{3}{4} \times 1 + \frac{2}{5} \times \frac{1}{4} \times 3 = \frac{3}{4}.$$

The expected payoff of Player 2 on mixed strategy $p = (p_1, p_2)$:

$$\frac{3}{5} \times \frac{3}{4} \times 2 + \frac{3}{5} \times \frac{1}{4} \times 4 + \frac{2}{5} \times \frac{3}{4} \times 5 + \frac{2}{5} \times \frac{1}{4} \times 2 = \frac{16}{5}.$$

2.3.2 例子2:D

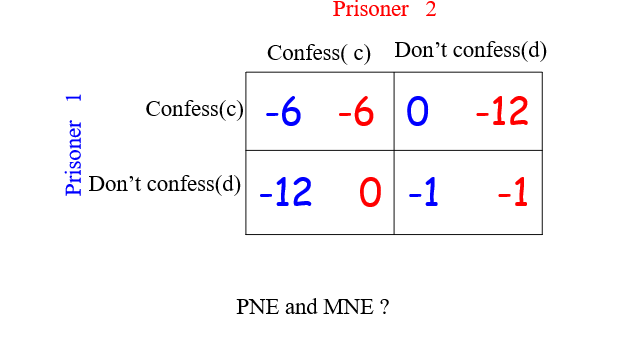
PNE:(C,C)

Mixed Nash Equilibrium:No

2.3.2 例子3:Primitive Hunting

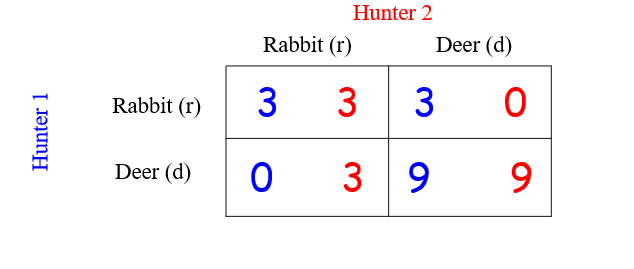
PNE:(3,3);(9,9)

Mixed Nash Equilibrium: NO

2.3.2 例子4:Rock-Paper-Scissors

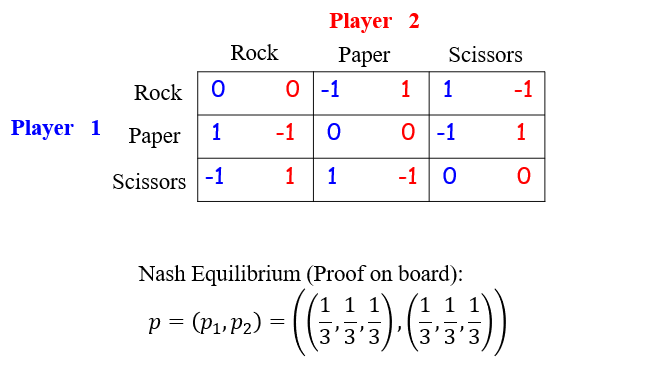
第一步：猜测某些行和列（正概率）

• 在这个步骤中，你需要猜测一些可能的策略（即猜测某些行和列将具有正的概率）。例如，你可以从猜测博弈矩阵中的某些行或列在混合策略中的概率为正开始。
• 这些猜测基于一个假设：玩家会随机选择他们的纯策略，目的是选择你认为可能在均衡中具有非零概率的几种策略（行或列）。

第二步：计算混合策略

• 在这个步骤中，你需要计算每个玩家的混合策略。混合策略是一个玩家可用纯策略的概率分布。
• 例如，如果玩家1有两个策略$U$和$D$，他们的混合策略可能是$p_1 = (p, 1-p)$，其中$p$是选择$U$的概率，而$(1-p)$是选择$D$的概率。你需要通过计算得出这些概率，使得两个玩家的策略都最优。

第三步：检查纳什均衡

• 一旦你计算出了混合策略，就需要检查这些策略是否形成了纳什均衡。这意味着你需要验证在其他玩家的策略保持不变的情况下，任何玩家都无法通过改变自己的策略来提高自己的收益。换句话说，你需要确保每个玩家的策略都是对方策略的最优回应。

运行时间随着策略数量指数增长

• 这个方法之所以可能需要指数级的时间，是因为你需要检查大量可能的策略组合。如果每个玩家有$n$种纯策略，那么混合策略的可能组合数量随着$n$的增大而指数增长。因此，你可能需要评估大量的策略组合来找到纳什均衡，计算量随着策略数量的增加而变得非常大。

纳什均衡有奇数性质