第三章支配策略和理性

[TOC]

3.1 Kakutani Fixed Point Theorem

Let $f: A \to A$ be a correspondence with $f(x) \subset A$ for $x \in A$. If:

A is compact, convex, and non-empty (finite space)
- 紧致意味着集合 A 是有界的并且包含所有的极限点。
- 凸意味着对于集合 A 中的任意两个点 $x_1, x_2$，它们之间的连线上的所有点也属于 A。这
- 非空意味着集合 A至少包含一个点。
f(x) is non-empty for all $x \in A$
- 这意味着，对于集合 A 中的每一个点 x，我们都能找到至少一个点 y 使得 $y \in f(x)$。简单来说，每个点都有一个映射值。
f(x) is a convex set
- 对于集合 A 中的每一个点x，f(x) 是一个凸集。换句话说，如果$y_1, y_2 \in f(x)$，那么对于任意 $\lambda \in [0, 1]$，组合点 $\lambda y_1 + (1-\lambda) y_2 $也属于 f(x)。
f(x) has a closed graph: if $\{x_n, y_n\} \to \{x, y\}$ and $y_n \in f(x_n)$, then $y \in f(x)$
- 闭图性意味着，如果一个序列 $\{x_n, y_n\} \to \{x, y\}$，且每个$y_n \in f(x_n)$，那么 y 必定属于 f(x)。
- 换句话说，如果我们通过极限过程从 $x_n$ 收敛到 x，并且在每个点$x_n$ 上找到一个 $y_n \in f(x_n)$，那么最终 y 会收敛到 f(x) 中的某个点。

then, there is an $x \in A$ such that $x \in f(x)$.

在满足以上条件的情况下，Kakutani 固定点定理保证存在一个点 $x \in A$，使得$x \in f(x)$，即 x是一个固定点。这意味着存在一个点 x，它的映射值恰好是它本身，或者换句话说，f(x) = x。

博弈论：在博弈论中，Kakutani 固定点定理经常被用来证明混合策略纳什均衡的存在。通过构造一个适当的映射函数，可以使用该定理来证明在某些博弈中必然存在一个均衡点。

3.1.1 Sketch 证明纳什均衡的存在性

A mixed outcome p is a NE iff $p \in B(p)$

$B(p) = B_1(p_{-1}) \times B_2(p_{-2}) \times \dots \times B_N(p_{-N})$

$B(p): \Delta(A_1) \times \dots \times \Delta(A_N) \to \Delta(A_1) \times \dots \times \Delta(A_N)$

$\Delta(A_1) \times \dots \times \Delta(A_N) $is compact, convex, and non-empty
B(p) is non-empty for all p;
B(p) is a convex set;
B(p) has a closed graph: if $\{ p^n, \hat{p}^n \} \to \{ p, \hat{p} \}$ and $\hat{p}^n \in B(p^n)$, then $\hat{p} \in B(p)$

then, there is a $p \in \Delta(A_1) \times \dots \times \Delta(A_N) $such that $p \in B(p)$

3.1.2 证明

证明1：$\Delta(A_1) \times \dots \times \Delta(A_N) $is compact, convex, and non-empty

Let $n = |A_i|$（即 $A_i$的元素个数为 n）. Then

$\Delta(A_i) = \left\{ (x_1, \dots, x_n) : x_i \in [0, 1], \sum_{i} x_i = 1 \right\}$

is a simplex of dimension $n-1$（这个集合是一个维度为 n−1 的单纯形。）

单纯形：是由一组点通过直线段、面或超平面连接形成的凸包

证明2：B(p) is non-empty for all p

$B_i(p_{-i}) = \arg \max_{p_i’ \in \Delta(A_i)} U_i(p_i’, p_{(-i)})$

Let $f(x) = U_i(x, p_{(-i)}) = \sum_k x_k U_i(p_{(-i)}, a_k) \quad \text{for} \quad x \in \Delta(A_i)$

f(x) 即表示玩家 i在混合策略下的期望效用。

f(x) is continuous, and $\Delta(A_i)$ is a non-empty compact set.

前者上个笔记证明了，后者是证明1

By the Weierstrass Theorem, f(x) has a maximum in $\Delta(A_i)$.

Weierstrass 定理（Weierstrass Theorem）:如果一个函数在一个紧致集合上是连续的，那么它一定有最大值

Thus, $B_i(p_{-i}) = \arg \min_{x \in \Delta(A_i)} f(x)$ is non-empty.

证明3：f(x) is a convex set

For any $\lambda \in [0,1],$ if $p_i’, p_i’’ \in B_i(p_{-i})$, then we need to prove that

$\lambda p_i' + (1 - \lambda) p_i'' \in B_i(p_{-i})$$（根据定义得到） From $ p_i', p_i'' \in B_i(p_{-i}) $, we have: $$U_i(p_i, p_{(-i)}) \geq U_i(p_i^*, p_{(-i)}) \quad \text{for all } p_i^* \in \Delta(A_i),$ $U_i(p_i', p_{(-i)}) \geq U_i(p_i^*, p_{(-i)}) \quad \text{for all } p_i^* \in \Delta(A_i),$ $U_i(\lambda p_i' + (1 - \lambda) p_i'', p_{(-i)}) \geq U_i(p_i^*, p_{(-i)}) \quad \text{for all } p_i^* \in \Delta(A_i)$

Proof:

$U_i(\lambda p_i’ + (1 - \lambda) p_i’’, p_{(-i)}) \geq \lambda U_i(p_i’, p_{(-i)}) + (1 - \lambda) U_i(p_i’’, p_{(-i)})$
$\geq \lambda U_i(p_i^, p_{(-i)}) + (1 - \lambda) U_i(p_i^, p_{(-i)}) = U_i(p_i^*, p_{(-i)})$

证明4：if $\{ p^n, \hat{p}^n \} \to \{ p, \hat{p} \}$ and $\hat{p}^n \in B(p^n)$, then $\hat{p} \in B(p)$

Assume $(p^n, \hat{p}^n) \to (p, \hat{p})$ and $ \hat{p}^n \in B(p^n)$ but $\hat{p} \notin B(p)$

There exists $\hat{p}_i \notin B_i(p_{(-i)})$ i.e., there exist $\bar{p}_i$ and$\epsilon > 0$ such that:

$U_i(\bar{p}_i, p_{(-i)}) \geq U_i(\hat{p}_i, p_{(-i)}) + 3\epsilon$

同时存在一个策略$\bar{p}_i$ 和一个正的 $\epsilon$ 满足如上所示

For continuous $U_i, p_{(-i)}^n \to p_{(-i)} $ and $(\hat{p}_i^n, p_{(-i)}^n) \to (\hat{p}_i, p_{(-i)})$

$U_i(\bar{p}_i, p_{(-i)}^n) > U_i(\bar{p}_i, p_{(-i)}) - \epsilon$ $U_i(\hat{p}_i, p_{(-i)}) > U_i(\hat{p}_i^n, p_{(-i)}^n) - \epsilon$

因为效用函数是连续的，因此存在如上所示

We have $U_i(\bar{p}_i, p_{(-i)}^n) > U_i(\hat{p}_i^n, p_{(-i)}^n) + \epsilon$,thus $\hat{p}_i^n \notin B_i(p_{(-i)}^n)$

3.2 Dominant Strategy

For some special cases, there is a optimal strategy independent of others’ choice, e.g., dominant strategy

和纳什均衡的区别：纳什均衡强调的是在给定其他玩家策略的情况下，没有任何玩家可以通过单方面改变策略来获得更好的结果；而支配策略则是指无论其他玩家选择什么策略，某个玩家的某个策略总是比其他策略更好。

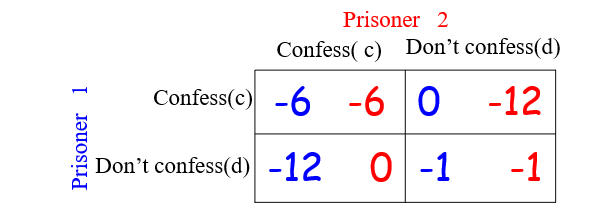
如图，Prisoner 2 will select c whatever Prisoner 1 how to choose（因此c就是一个支配策略）.

3.2.1 正式定义

$a_{(-i)} = (a_1, \dots, a_{i-1}, a_{i+1}, \dots, a_N) $is the outcome of strategies taken by all players other than i

$ A_{(-i)} $denotes the set of all such outcomes.

A pure strategy $a_i $ strictly dominates $ a_i’ $ if
$u_i(a_i, a_{(-i)}) > u_i(a_i', a_{(-i)}) \quad \text{for all} \quad a_{(-i)} \in A_{(-i)}$
A pure strategy $a_i $ weakly dominates $a_i’$ if
$u_i(a_i, a_{(-i)}) \geq u_i(a_i', a_{(-i)}) \quad \text{for all} \quad a_{(-i)} \in A_{(-i)}$
while $u_i(a_i, a_{(-i)}) > u_i(a_i’, a_{(-i)}) $for some $a_{(-i)} \in A_{(-i)}$

$a_i$ is strictly dominant if it strictly dominates all other strategies in $ A_i $, and it is called weakly dominant if it weakly dominates all other strategies in $ A_i $.

3.3 Dominant Strategy Equilibrium 支配策略均衡

If every player has a (strictly and weakly) dominant strategy, then the corresponding outcome is a (strictly and weakly) dominant strategy equilibrium.支配策略的对应联合结果就是支配策略均衡

Dominant strategy equilibrium belongs to NE.

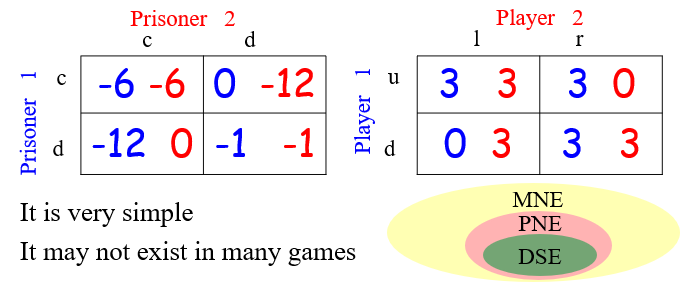
3.3.1 纳什均衡和支配策略均衡关系

纳什均衡不意味着博弈双方达到一个整体的最优状态，但需要注意的是，只有对玩家当前选择的最优策略才可以达到纳什均衡，严格劣势策略不可能成为最佳对策，而弱优势和弱劣势策略可能达到纳什均衡。

双方都支配的策略一定是纳什均衡，但反之不一定。

反例：性别战（Battle of the Sexes）

	玩家B：足球	玩家B：歌剧
玩家A：足球	(3, 2)	(0, 0)
玩家A：歌剧	(0, 0)	(2, 3)

纳什均衡：
- 当玩家A选择“足球”，玩家B选择“足球”时，玩家A没有动力单方面改变策略（因为3 > 0），玩家B也没有动力单方面改变策略（因为2 > 0）。因此，（足球，足球）是一个纳什均衡。
- 类似的，（歌剧，歌剧）也是一个纳什均衡。
支配策略：
- 对于玩家A来说：
  - 如果玩家B选择“足球”，玩家A选择“足球”更好（3 > 0）。
  - 如果玩家B选择“歌剧”，玩家A选择“歌剧”更好（2 > 0）。
  - 因此，玩家A没有支配策略，因为最优策略取决于玩家B的选择。
- 对于玩家B来说情况相同

存在两个纳什均衡：（足球，足球）和（歌剧，歌剧）。
但没有任何玩家有支配策略，因为每个玩家的最优策略都依赖于对方的选择。

3.4 Second Price Auction

第二价格拍卖\维克里拍卖

N: players bid a building

$v_i≥0$: the true value for player i

$b_i≥0$: the bid price(竞标价格) for player i

$v_i-b_i$: the payoff for player i

The rule of second-price auction is given as follow:

Players make bids $b=(b_1,b_2,…,b_N)$ simultaneously
The higher player wins the building, yet pays the second highest bid price 最高的获得拍卖品并支付第二高的价格
If there are more than one highest players, then randomly select one player and pay his own bid price

3.4.1 Theorem

In second price auction, the strategy $b_i=v_i$ is a weakly dominant strategy for each player i.

$(v_1,v_2,…,v_N)$ is a weakly dominant strategy equilibrium

Proof：

It suffices to show $u_i(v_i, b_{(-i)}) \geq u_i(b_i, b_{(-i)})$ for all b_i, b_{(-i)}

If someone’s bid $b_k \geq v_i $, then player i has to pay $ b_i > b_k \geq v_i $ by winning. The payoff is $ v_i - \max_{k \neq i} b_k \leq 0 $. It is optimal to select $ b_i = v_i $

If each bid price $ b_k < v_i $, then the payoff is $ v_i - \max_{k \neq i} b_k > 0 $, since the payoff is always the same when winning. It is optimal to select $ b_i = v_i $

3.4.2 some notes

Honesty strategy is the best strategy

Many internet auctions can be regarded as variants of second price auction.

许多互联网拍卖可以视为第二价格拍卖的变种

How about the first price auction. Is it a dominant strategy to bid your true value?

在第一价格拍卖中，最高出价者赢得拍卖并支付他们出价的金额。出价自己的真实价值（即出价正好等于物品对自己来说的价值）在这种拍卖格式中不是一个占优策略。
在第一价格拍卖中，竞标者通常有动机少出价（即出价低于真实价值），以增加他们的盈余（如果他们赢得拍卖）。出价自己的真实价值不是最优策略，因为通过稍微少出价通常能得到更好的结果。

3.5 Dominated Strategies

A pure strategy $a_i$ strictly dominates $a_i’\to $ $a_i’$ is strictly dominated by $a_i$ if:

$u_i(a_i, a_{(-i)}) > u_i(a_i', a_{(-i)}) \quad \text{for all} \quad a_{(-i)} \in A_{(-i)};$

$a_i$ weakly dominates $a_i’\to$ $a_i’$ is weakly dominated by $a_i$ if:

$u_i(a_i, a_{(-i)}) \geq u_i(a_i', a_{(-i)}) \quad \text{for all} \quad a_{(-i)} \in A_{(-i)}$ $\text{while} \quad u_i(a_i, a_{(-i)}) > u_i(a_i', a_{(-i)})\quad \text{for some} \quad a_{(-i)} \in A_{(-i)}.$

3.6 Iterated Elimination of Dominated Strategies

如何找到主导策略均衡？支配策略的迭代删除（Iterated Elimination of Dominated Strategies）

If every strategy eliminated is a strictly dominated strategy 如果每一个被删除的策略都是严格支配的策略，称为严格支配策略的迭代删除
- Iterated elimination of strictly dominated strategy
If at least one strategy eliminated is a weakly DS 如果至少有一个被删除的策略是弱支配的策略，称为弱支配策略的迭代删除
- Iterated elimination of weakly dominated strategy

3.7 Mixed Strategy and Dominant Strategy

3.7.1 Belief

Given a strategy game $G = \{N, \{A_i\}, \{u_i\}\}$ .

A mixed strategy outcome $p = (p_1, p_2, \dots, p_N$) .

$p = (p_i, p_{-i}) $, $ p_{-i}$ is called a belief.

注意这里的 $ p_{-i}$ 是某个player混合策略选择中的概率情况，并不是之前的整体均衡

A belief $p_{-i} $ of player $i$ is a probability over $A_{-i}$.

A strategy $a_i \in A_i$ is a best response to belief $p_{-i}$ if:

$U_i(a_i, p_{-i}) \geq U_i(a, p_{-i}) \quad \text{for all } a \in A_i.$

辨析:混合策略中的符号

$p=(p_1,p_2,…,p_n)$ 是所有玩家的一个混合策略空间，对于每个玩家有 $p_i = (p_{i1}, p_{i2}, \dots, p_{i n_i}) $，这里的$p_i$就是上文中的$p$，belief的定义也来源于此。

3.7.2 Rationality and NE

A pure strategy $a_i \in A_i$ is rational if there exists a belief $p_{-i}$ such that $a_i$ is a best response to the belief $p_{-i}$.

Theorem: Every pure strategy with positive probability in a mixed strategy Nash equilibrium is rational.混合策略中任何一个正概率的纯策略都是理性的（混合策略自然也是理性的）

Proof: Let $p = (p_1, p_2, \dots, p_N)$ be a mixed strategy Nash equilibrium. Then, $p_i$ is a best response to $p_{-i}$, and every strategy with positive probability in $p_i$ is also a best response to $p_{-i}$.

3.7.3 Rationality and Strictly Dominant Strategy

$a_i \in A_i$ is rational if $a_i$ is a best response to some belief $p_{-i}$:

$U_i (a_i, p_{-i}) \geq U_i (a, p_{-i}) \quad \text{for all } a \in A_i$

A mixed strategy $p_i \in \Delta(A_i)$ strictly dominates $a_i \in A_i$ if:

$U_i (p_i, p_{-i}) > U_i (a_i, p_{-i}) \quad \text{for all } p_{-i} \in \Delta(A_{-i})$

Theorem：If a strategy $a_i \in A_i$ is rational, then $a_i$ is not strictly dominated. 理性策略一定不被严格占优

By contradiction: Assume that $a_i’ \in A_i$ strictly dominates $a_i$：

$U_i (a_i', p_{-i}) > U_i (a_i, p_{-i})$

3.7.4 Rationalizability

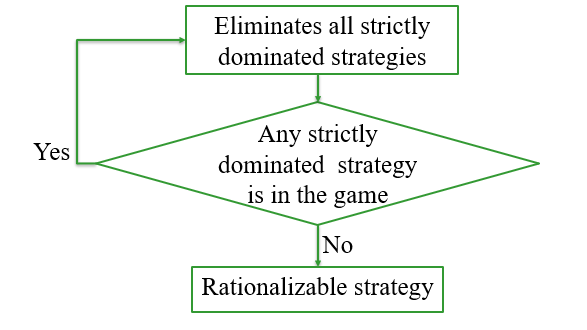
Eliminate all strictly DS and keep weakly DS
Eliminate all strictly DS by pure and mixed strategy

3.8 一些例子

3.8.1 例1:

Iterated Elimination and Pure Dominate Strategy

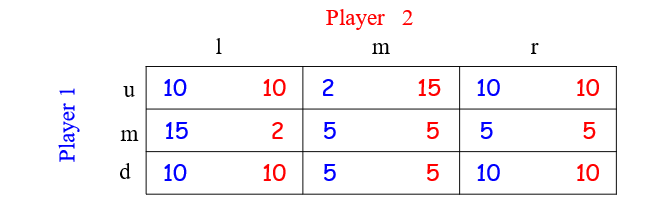
For player 1, the strategy ‘u’ is weakly dominated by ‘d’
For player 2, the strategy ‘l’ is weakly dominated by ‘r’

Therefore,we have the game

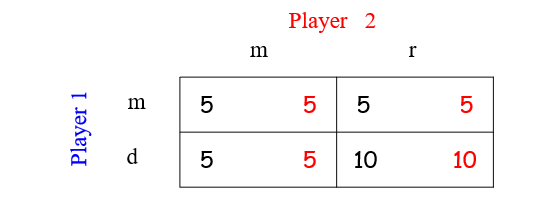
For player 1, the strategy ‘m’ is weakly dominated by ‘d’
For player 2, the strategy ‘m’ is weakly dominated by ‘r’

By iterated elimination of weakly dominated strategy

(d,r) is a weakly dominant strategy Equilibrium

3.8.2 例2：

Mixed Strategy and Dominant Strategy

A strategy may be not dominated by other strategies, yet can be dominated by a mixed strategy

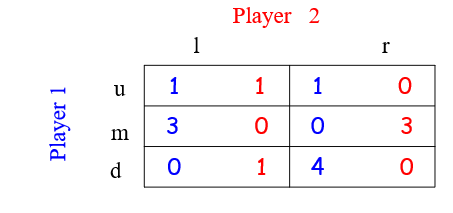
For player 1, no strategy dominates ‘u’
The mixed strategy $p_1=(0, 0.5, 0.5)$ dominates ‘u’

Figure out the dominated strategy for expected payoff

Let $p_2=(p,1-p)$ be the mixed strategy for player 2

$U_1 (u,p_2 )=1$

$U_1 (m,p_2 )=3p $

$U_1 (d,p_2 )=4(1-p)$

3.8.3 Example 3

Mixed Strategy and Dominant Strategy

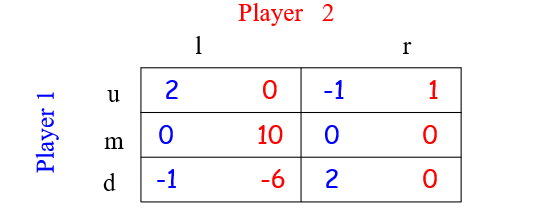
Player 1 is rational

m被$(\frac{1}{2},0,\frac{1}{2})$严格占优，不会选

Player 2 is rational and knows that Player 1 is rational

类似的，r不会被选

Player 1 is rational, and knows that player 2 is rational, and knows that 2 knows that 1 is rational

以此类推，可以不断迭代删除，最后获得理性策略(d,r)

3.8.4 Example 4：Beauty Contest (选美竞赛游戏)

There are $n$ players.
Each player selects a number $a_i \in [0, 50]$.
The payoff for each player $i$ is given by: $\pi_i = 50 - \left( a_i - \frac{2}{3} \frac{\sum_{i} a_i}{n} \right)^2$

Given $a_{-i}$, the best strategy for player $i$ is: $a_i^* = \frac{2}{3} \frac{\sum_{j, j \neq i} a_j}{n - \frac{2}{3}}$

And the optimal $a_i^$ lies within the range:$$ a_i^ \in \left[ 0, \frac{2}{3} \frac{n - 1}{n - \frac{2}{3}} 50 \right] $$

After round 1: $ \left[ 0, \frac{2}{3} \frac{n-1}{n-\frac{2}{3}} 50 \right] $

After round 2: $ \left[ 0, \left( \frac{2}{3} \frac{n-1}{n-\frac{2}{3}} \right)^2 50 \right] $

After round k: $ \left[ 0, \left( \frac{2}{3} \frac{n-1}{n-\frac{2}{3}} \right)^k 50 \right] $

…

Rational = $\{0\}$

3.9 Theorem

Theorem:A strictly dominated strategy is never used with positive probability in a mixed strategy Nash equilibrium

定理： 严格被支配的策略在混合策略纳什均衡中永远不会被以正概率采用。

假设玩家 i 在混合策略均衡中以正概率 p > 0 选择严格被支配策略 $a_i$ ，而存在严格支配策略 $ a_i’$。

根据严格支配的定义，对于所有 $ a_{-i}$，有：
$u_i(a_i’, a_{-i}) > u_i(a_i, a_{-i})$
若玩家 i将原本分配给 $a_i$ 的概率 $p$ 转移到 $a_i’$，则他的期望收益会严格增加，与纳什均衡的稳定性矛盾。

3.9.1 例3：Find Mixed Strategy Nash Equilibria

Step 1: eliminate all strictly dominated strategies (mixed)

Step 2: use our previous methods introduced in Chapter 2

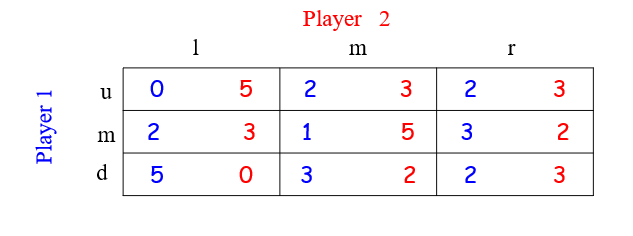
3.9.2 例4：Find Mixed Strategy Nash Equilibria

3.10 一些其他博弈

3.10.1 Symmetric Game 对称博弈

A game is symmetric if any player’s payoff $u_i(a_i, a_j, a_{-i,j})$ can be converted into any other player’s payoff $u_j(a_j, a_i, a_{-i,j})$ simply by re-arranging the player’s “names”.

Theorem. Any symmetric game has a symmetric NE, where each player uses the same strategy

3. 10.2 Continuous Game

A game $G = \{ N, \{ A_i \}, \{ u_i \} \}$ with complete information is continuous if each $A_i$ is non-empty and compact, and $u_i: A \to \mathbb{R}$ are continuous.

Cournot game $ \dots$

Many quantities are essentially continuous: If we’re considering how many fish to catch in a season, where the measurement is in millions of tons.

3.10.3 Existence of Equilibria for Infinite Games

(Nash) Every finite game has a mixed strategy Nash equilibrium.

(Debreu, Glicksberg, Fan) Consider a strategic form game $ \{ N, \{ A_i \}, \{ u_i \} \} $ such that for each player:

$ A_i $ is compact and convex.
$ u_i(a_i, a_{-i}) $ is continuous in $ a_{-i} $.
$ u_i(a_i, a_{-i}) $ is continuous and concave in $ a_i $.

There exists a pure strategy Nash equilibrium.

3.10.4 More Powerful Theorem

(Glicksberg) Consider a strategic form game $ \{ N, \{ A_i \}, \{ u_i \} \} $ such that for each player:

$ A_i $ is compact and convex.
$ u_i(a) $ is continuous in $ a $.

There exists a mixed strategy Nash equilibrium.

For continuous pure strategy space, the space of mixed strategy has infinite dimension