第五章 Games with Incomplete Information

[TOC]

5.1 引入：Battle of Sexes with Incomplete Information

• 完全信息的情况下，我们知道：both boy and girl like to meet

• There are 2 pure strategy NE and 1 mixed strategy NE

• IF:The boy is not sure if the girl wishes to meet or not

  Incomplete information

5.1.1 detail

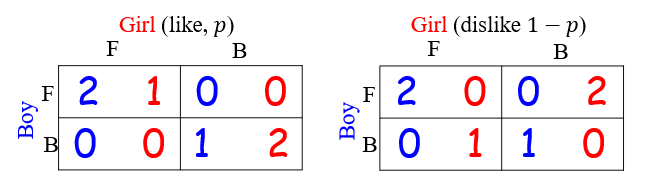
The girl has two types: like or dislike

The boy assumes that girl like with probability p

The girl knows the complete information

The boy does not know

5.1.2 NE

If the boy selects $B$, then the best response of the girl is $(B,F)$. Thus, the strategy pair is: $\{B, (B,F)\}$

$U_1 (B,(B,F)) = p + (1 - p) \cdot 0 = p$

$U_1 (F,(B,F)) = 0 + (1 - p) \cdot 2 = 2(1 - p)$

If $p \geq \frac{2}{3}$, then $\{B, (B,F)\}$ is a Nash Equilibrium (NE).

If $p < \frac{2}{3}$, then $\{B, (B,F)\}$ is not a NE.

If the boy selects $F$, then the best response of the girl is $(F,B)$. Thus, the strategy pair is: $\{F, (F,B)\}$

$U_1 (F,(F,B)) = 2p + (1 - p) \cdot 0 = 2p$

$U_1 (B,(F,B)) = 0 + (1 - p) = 1 - p$

If $p \geq \frac{1}{3}$, then $\{F, (F,B)\}$ is a Nash Equilibrium (NE).

If $p < \frac{1}{3}$, then $\{F, (F,B)\}$ is not a NE.

If $p \geq \frac{1}{3}$ then$ \{F, (F,B)\} $ is a Nash Equilibrium $NE$.

If $p \geq \frac{2}{3} $, then both $\{F, (F,B)\}$ and $\{B, (B,F)\}$ are Nash Equilibriums (NEs).

5.2 Bayesian Games

A Bayesian game consists of:

• A set of players N
• A set of strategies $A_i$ for each player i
• A set of types $\Theta_i$ for each player i
  • The type set $\Theta_i$ includes all private information for player i
  • The types on payoff are adequate (Payoff types)
• A probability distribution $p = p(\theta_1, \dots, \theta_N)$ on $i\prod_{i=1}^{n} \Theta_i$

For player $i$, a pure strategy is a map $a_i : \Theta_i \to A_i$, which prescribes a strategy for each type:

$$a_i = \left( a_i(\theta_i^1), a_i(\theta_i^2), \dots, a_i(\theta_i^{n_i}) \right)$$

A payoff function $u_i : \prod_{i=1}^{N} A_i \times \prod_{i=1}^{n} \Theta_i \to \mathbb{R}$ is defined as:

$$u_i(a_1, \dots, a_N, \theta_1, \dots, \theta_N) \quad \text{for } a_i \in A_i \text{ and } \theta_i \in \Theta_i$$

The game $G$ is defined as:

$$G = \left\{ N, \{ A_i \}, \{ \Theta_i \}, \{ u_i \}, p \right\}$$

5.2.1 Battle of Sexes with Incomplete Information

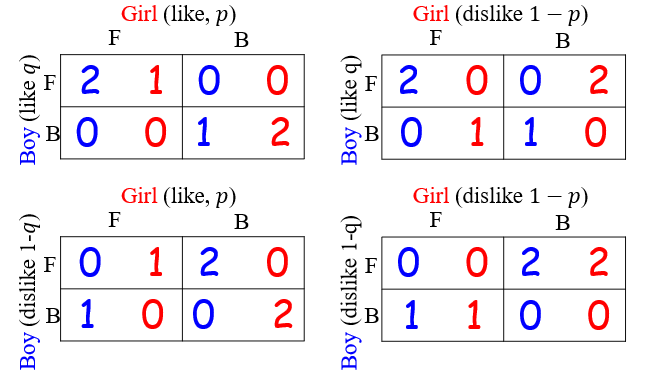
5.2.2 Such game is called Bayes Game

The set of types $ \Theta_i $ for each player $ i $.

• Player $ i $ does not know the selection of $ \Theta_j $.

• All types are drawn from the prior distribution $ p(\theta_1, \dots, \theta_N) $:
• $p(\theta_1, \dots, \theta_N) = p(\theta_1) p(\theta_2) \dots p(\theta_N) $ independent types

Given $ p(\theta_1, \dots, \theta_N) $, we have, by Bayes’ rule:

$$p(\theta_{(-i)} | \theta_i) = \frac{p(\theta_i, \theta_{(-i)})}{p(\theta_i)}$$

where $ \theta_{(-i)} = (\theta_1, \dots, \theta_{i-1}, \theta_{i+1}, \dots, \theta_N) $.

Such a game is called a Bayes Game.

5.2.3 Outcome and Payoff Functions

A pure strategy for player $i$ is:

$$(a_i (\theta_i^1), a_i (\theta_i^2), \dots, a_i (\theta_i^{n_i}))$$

An outcome of the Bayes game is given by:

$$((a_1 (\theta_1^1), \dots, a_1 (\theta_1^{n_1})), \dots, (a_N (\theta_N^1), \dots, a_N (\theta_N^{n_N})))$$

Given $a_{-i}$, the expected payoff of player $i$ and type $\theta_i$ is:

$$U_i (a_i (\theta_i), a_{(-i)}) = \sum_{\theta_{(-i)}} p(\theta_{(-i)} | \theta_i) u_i (a_{(-i)} (\theta_{(-i)}), a_i, \theta_{(-i)}, \theta_i)$$

5.3 Bayesian Nash Equilibrium

Definition: The outcome $(a_1, a_2, \dots, a_N)$ is a Bayesian Nash Equilibrium if for each $i$ and type $\theta_i$, we have:

$$U_i (a_i (\theta_i), a_{(-i)}) \geq U_i (a_i' (\theta_i), a_{(-i)}) \quad \text{for all } a_i' (\theta_i) \in A_i$$

Given $a_{(-i)}$ and type $\theta_i$, the best response for player $i$ is:

$$\begin{align*} B_i (a_{(-i)}, \theta_i)& = \{ a_i (\theta_i) : U_i (a_i (\theta_i), a_{(-i)})\\& \geq U_i (a_i' (\theta_i), a_{(-i)}) \quad \text{for all } a_i' (\theta_i) \in A_i \} \end{align*}$$

Theorem: The outcome $(a_1, a_2, \dots, a_N)$ is a Bayesian NE if and only if for every player $i$ and each type $\theta_i$, we have:

$$a_i (\theta_i) \in B_i (a_{(-i)}, \theta_i)$$

5.3.1 How to find Bayesian Nash Equilibrium

Find the best response function for each player and type.

Find the Bayesian Nash Equilibrium by $a_i(\theta_i \in B_i(a_{(-i)}, \theta_i) $.

5.4 例1:Bank Runs (银行挤脱)

Both players 1 and 2 have a deposit of $100 in the bank.

If the bank manager is good, each player gets $150; if the manager is bad, then they lose all their money.

Players can withdraw money, but the bank has only $100.

• If only one player withdraws, he gets $100 and the other gets 0.
• If two players both withdraw, each gets $50.

Player 1 believes the manager is good with probability p .

Player 2 knows whether the manager is good or bad.

Both players simultaneously make a strategy: withdraw or not.

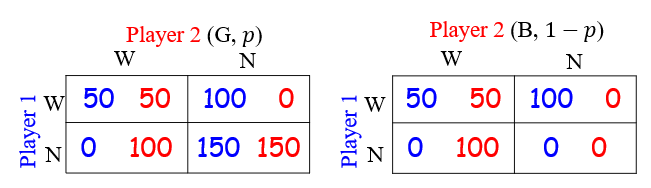
• Two players

• Strategies $A_1 = A_2 = \{ W, N \} $

• Types $ \Theta_1 = \{ 1 \} ; \Theta_2 = \{ G, B \} $

A probability distribution $p_1(\theta_2 = G) = p $

Payoffs:

• Player 1: W or N
• Player 2: W(G), N(G), W(B), N(B)

5.4.1 Bayesian Nash Equilibrium of Bank Runs

case 1

If Player 1 selects $ W $, then

$$B_2(W, G) = \{W\}, \quad B_2(W, B) = \{W\}$$

Outcome $ (W, (W(G), W(B))) $: best strategy for Player 2.

Is $ W $ a best response to $ W(G), W(B) $?

$$U_1(W, (W(G), W(B))) = 50p + 50(1 - p) = 50$$ $$U_1(N, (W(G), W(B))) = 0p + 0(1 - p) = 0$$

$ (W, (W(G), W(B))) $ is a Bayesian NE.

case 2

If Player 1 selects $ N $, then

$$B_2(N, G) = \{N\}, \quad B_2(N, B) = \{W\}$$

Outcome $ (N, (N(G), W(B))) $: Player 2 makes best strategy.

Is $ N $ a best response to $ (N(G), W(B)) $?

$$U_1(N, (N(G), W(B))) = 150p + 0(1 - p) = 150p$$ $$U_1(W, (N(G), W(B))) = 100p + 50(1 - p) = 50(1 + p)$$

If $ 150p > 50 + 50p $, then $ (N, (N(G), W(B))) $ is a Bayesian Nash Equilibrium (BNE).

5.5 例2:Cournot Duopoly with Incomplete Information

5.5.1 base situation

Two firms $ N = \{ 1, 2 \} $

Firm 1 has a cost $ c_H $;

Firm 2 has two costs $ c_L $ and $ c_H $

Firm 1 believes that Firm 2 selects $ c_H $ with probability $ p $

Firm 1’s strategy: $ \{ q_1 : q_1 \geq 0 \} $

Firm 2’s strategy: $ \{ q_{2,L}, q_{2,H} : q_{2,L} \geq 0 \text{ and } q_{2,H} \geq 0 \} $

Price: $ a - q_1 - q_{2,L} $ or $ a - q_1 - q_{2,H} $

5.5.2 payoff function

For player 1, the expected payoff function is

$$U_1 (q_1, q_{2,L}, q_{2,H}, c_L, c_H) = p q_1 (a - q_1 - q_{2,H}) + (1 - p) q_1 (a - q_1 - q_{2,L}) - c_H q_1$$

For player 2, the expected payoff function of type $ c_H $ is

$$U_2 (q_1, q_{2,H}, c_H) = (a - q_1 - q_{2,H}) q_{2,H} - c_H q_{2,H}$$

For player 2, the expected payoff function of type $ c_L $ is

$$U_2 (q_1, q_{2,L}, c_L) = (a - q_1 - q_{2,L}) q_{2,L} - c_L q_{2,L}$$

5.5.3 Best Response for Player 1

For player 1, the expected payoff function is

$$U_1 (q_1, q_{2,L}, q_{2,H}, c_L, c_H) = p q_1 (a - q_1 - q_{2,H}) + (1 - p) q_1 (a - q_1 - q_{2,L}) - c_H q_1$$

Maximizing $U_1 (q_1, q_{2,L}, q_{2,H}, c_L, c_H)$ gives

$$B_1 (q_{2,L}, q_{2,H}) = \left\{ \frac{a - p q_{2,H} - (1 - p) q_{2,L} - c_H}{2} \right\}$$

5.5.4 Best Response for Player 2

For player 2, the expected payoff function of type $c_H$ is

$$U_2 (q_1, q_{2,H}, c_H) = (a - q_1 - q_{2,H}) q_{2,H} - c_H q_{2,H}$$

Maximizing $U_2 (q_1, q_{2,H}, c_H)$ gives

$$B_2 (q_1, c_H) = \left\{ \frac{a - q_1 - c_H}{2} \right\}$$

Similarly, we have

$$B_2 (q_1, c_L) = \left\{ \frac{a - q_1 - c_L}{2} \right\}$$

5.5.5 Bayesian Nash Equilibrium

$$B_1 (q_{2,L}, q_{2,H}) = \left\{ \frac{a - p q_{2,H} - (1 - p) q_{2,L} - c_H}{2} \right\}$$ $$B_2 (q_1, c_H) = \left\{ \frac{a - q_1 - c_H}{2} \right\}$$ $$B_2 (q_1, c_L) = \left\{ \frac{a - q_1 - c_L}{2} \right\}$$

We solve the Bayesian Nash Equilibrium by

$$q_1 \in B_1 (q_{2,L}, q_{2,H})$$ $$q_{2,H} \in B_2 (q_1, c_H)$$ $$q_{2,L} \in B_2 (q_1, c_L)$$

The Bayesian Nash Equilibrium is $(q_1, (q_{2,L}, q_{2,H}))$

$$q_1 = \frac{a - c_H - (1 - p)(c_H - c_L)}{3}$$ $$q_{2,H} = \frac{a}{3} - \frac{c_H + c_L}{6} - p \cdot \frac{c_H - c_L}{6}$$ $$q_{2,L} = \frac{a}{3} - \frac{c_L}{3} - p \cdot \frac{c_H - c_L}{6}$$

Discussions:

• Incomplete information affects the outputs of players.
• $q_{2,L} > q_{2,H}$ implies player 2 produces more for the lower price.

5.5.6 other discussions

If player 1 knows that player 2 selects $c_H$ ($p=1$) then

$$q_1 = q_{2,H} = \frac{a - c_H}{3}$$

If player 1 does not know the choices of player 2,

$$q_1 = \frac{a - c_H - (1 - p)(c_H - c_L)}{3}$$

If player 1 knows that player 2 selects $c_L$ ($p=0$) then

$$q_1 = q_{2,L} = \frac{a - c_L + c_H - c_L}{3}$$

If player 1 does not know the choices of player 2,

$$q_1 = \frac{a - c_L + c_H - c_L - (3 - p)(c_H - c_L)}{3}$$

Player 1 produces less with incomplete information.

If player 1 knows that player 2 selects $c_H$ ($p=1$) then

$$q_{2,H} = \frac{a - c_H}{3}$$

otherwise,

$$q_{2,H} = \frac{a - c_H}{3} + (1 - p) \frac{(c_H - c_L)}{6}$$

Player 2 benefits from the incomplete information.

The firm will benefit by keeping cost secrets.