[TOC]
6.1 引入
In some situation, players can observe others’ strategy before they make decision
- Simple Nim game
- There are n coins
- Two players select 1 or 2 or 3 coins in turn
- The winner is the one taking the last coin
6.1.1 比较
Strategy Game
Set of players
Set of strategies
Payoff functions
Extensive game provides more information
Sequences of players
Strategies available at different points in the game
Two variants
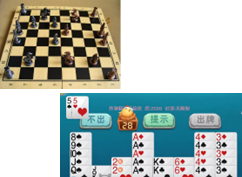
perfect information extensive-form games
国际象棋:知道对方所有可能的步骤
imperfect-information extensive-form games
扑克牌:不知道对方剩余的手牌和要出的牌的组合方式
6.1.2 Entry Game
A company G is trying to enter a new market
Another company B can either fight the entry or cooperate

Game Tree
node
- non-terminal node
- terminal node
branches
players
strategy
payoff
6.2 Formal Definition of Extensive Game
An extensive game with perfect information includes:
- Players: $N$ is the set of $N$ players
- Strategies: $A$ is a set of all strategies
- Histories: $H$ is a set of strategy sequences (finite or infinite) such that:
- The empty sequence $\emptyset \in H$
- If $a^1 a^2 \dots a^k \in H$, then $a^1 a^2 \dots a^s \in H$ when $s \leq k$
- If an infinite sequence $(a^k)_{k=1}^{\infty}$ satisfies $a^1 a^2 \dots a^k \in H$ for each positive $k$, then $(a^k)_{k=1}^{\infty} \in H$
6.2.1 example
$H=\{\emptyset,A,B,AL,AR\}$
6.2.2 extensive game with perfect information
- Players: $N$ is the set of $N$ players
- Strategies: $A$ is a set of all strategies
Histories: $H$ is a set of sequences (finite or infinite)
- Each sequence in $H$ is called a history; each component $a^i \in A$ is a strategy
- Terminal history: $a^1 \dots a^k \in H$ if $k = +\infty$ or $a^1 \dots a^{k+1} \notin H$ for any $a^{k+1} \in A$
- Terminal history set: $Z = \{\text{all terminal histories } a^1 \dots a^k \in H\}$
Player function: $P: H \setminus Z \to N$ assigns to each non-terminal history a player from $N$
- $P(h)$ denotes the player who takes action after the history $h$
- Payoff function: $u_i: Z \to \mathbb{R}$
- Game : $G = \{ N, H, P, \{ u_i \} \}$
6.2.3 Ultimatum Game
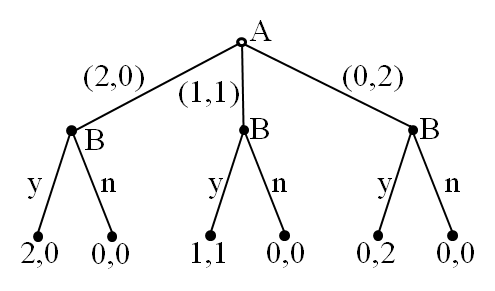
Game structure:
$G = \{ N, H, P, \{ u_i \} \}$
Players:
$N = \{ A, B \}$
Histories:
$H = \{ \emptyset, (2,0), (1,1), (0,2), ((2,0), y) \}
\cup \{ ((2,0), n), ((1,1), y), ((1,1), n) \}
\cup \{ ((0,2), y), ((0,2), n) \}$
Player function:
$P: P(\emptyset) = A; P((2,0)) = B; P((1,1)) = B; P((0,2)) = B$
Payoff functions:
$u_1((2,0), y) = 2, \quad u_1((2,0), n) = 0, \quad u_1((1,1), y) = 1, \quad u_1((1,1), n) = 0$
$u_2((2,0), y) = 0, \quad u_2((2,0), n) = 0, \quad u_2((1,1), y) = 1, \quad u_2((1,1), n) = 0$
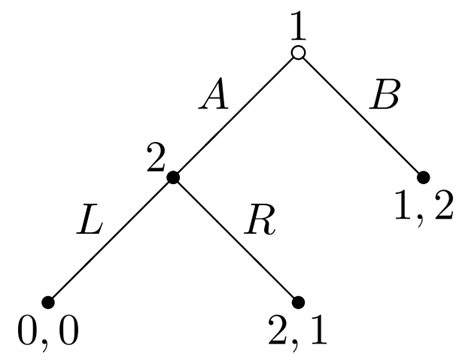
6.2.4 another example
Game structure:
$G = \{ N, H, P, \{ u_i \} \}$
Players:
$N = \{ 1, 2 \}$
Histories:
$H = \{ \emptyset, A, B, AL, AR \}$
Player function:
$P: P(\emptyset) = 1; P(A) = 2$
Payoff functions:
$u_1(B) = 1, \quad u_1(AL) = 0, \quad u_1(AR) = 2$
$u_2(B) = 2, \quad u_2(AL) = 0, \quad u_2(AR) = 1$
6.3 Pure strategies (注意是叉乘)
Definition: Given a game $G = \{ N, H, P, \{ u_i \} \}$, the pure strategy for player $i$ is given by the cross product
A pure strategy for a player is a complete specification of which deterministic action to take at every node belonging to that player.
6.3.1 例1
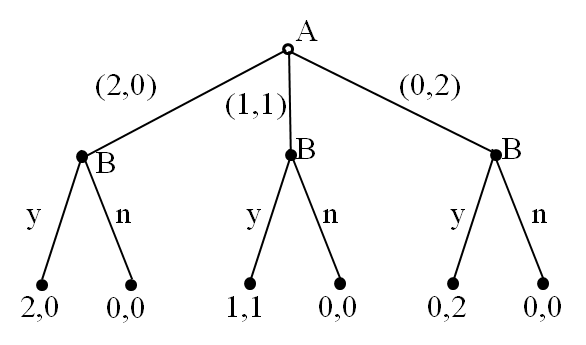
How many pure strategies for each player?
Player A: $(2,0), (1,1), (0,2)$
Player B: $\{yyy, yyn, yny, ynn, nyy, nyn, nny, nnn\}$
6.3.2 例2
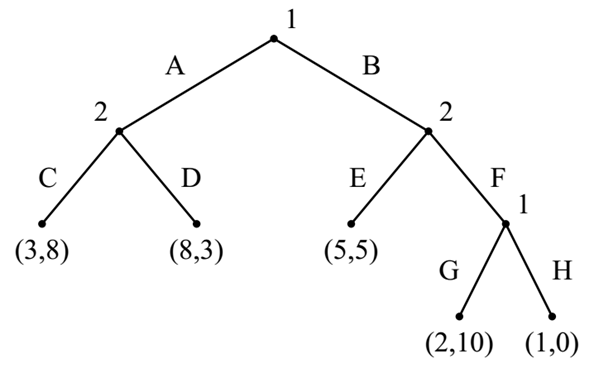
What are the pure strategies for players 1 and 2?
- Player 1: $\{AG,AH,BG,BH\}$
- Player 2: $\{CE,DE,CF,DF\}$
What are payoffs of each outcome for players 1 and 2?
$u_1(AG,CE) = 1$
(其实就是AC所在的这个决定,这是一个序列化的结果:如果1选择AG,那么另一边选择CE最终的收益,虽然GE是跑不到的,但是会做这样的一个理论上的选择)
6.4 NE 纳什均衡
Based on the definition of pure strategy, we can define
Mixed strategies
Best response
Nash equilibrium
Given an extensive game $G = \{ N, H, P, \{ u_i \} \}$, a strategy outcome $a^ = (a_1^, a_2^, \dots, a_N^)$ is a Nash equilibrium if and only if:
How to find Nash Equilibrium: Induced strategy game
6.4.1 a strategy game
Every extensive game can be converted to a strategy game
Remark: This conversion is not reverse 反过来是不能转化的:收益矩阵不能转化为动态博弈
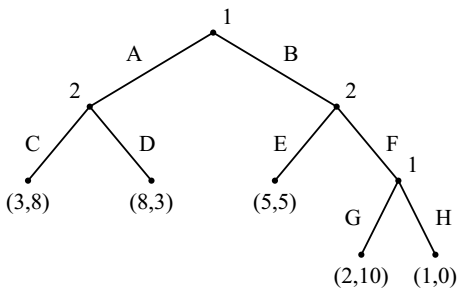
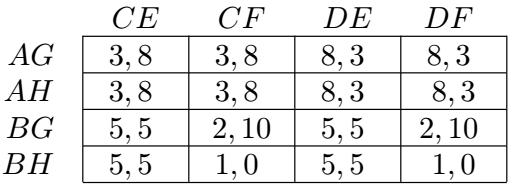
6.4.2 Kuhn Theorem (1953)
Theorem Every finite extensive game with perfect information has at least one Pure Strategy Nash Equilibrium (PSNE).
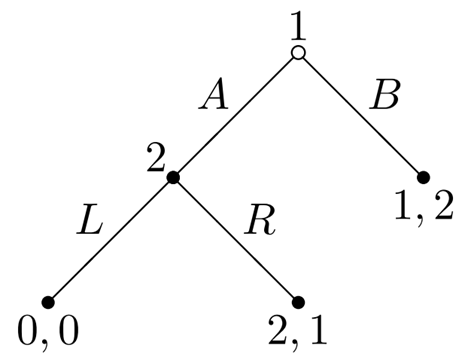
6.4.3 Example
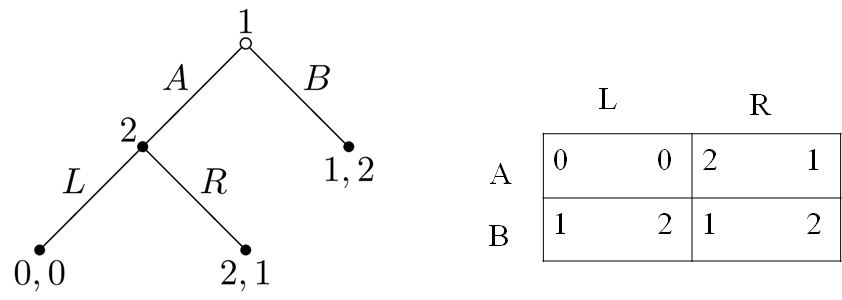
Nash Equilibria are $(B, L)$ and $(A, R)$.
- $(B, L)$ is a Nash equilibrium: if player 2 selects $L$, then player 1 selects $B$, and vice versa.
Is $(B, L)$ reasonable?
- $(B, L)$ is a non-credible threat.
指的是$(B, L)$这个$NE$的出现根本不可能:1选择B、2选择L这个出现不合情理也不够理性,非理性威胁现实中不会出现,用处不大。
6.4.4 Subgame (子博弈)
Definition A subgame is a set of nodes, strategies and payoffs, following from a single node to the end of game.
A subgame is a part of the game tree such that
It starts at a single strategy node
It contains every successor to this node
It contains all information in every successor
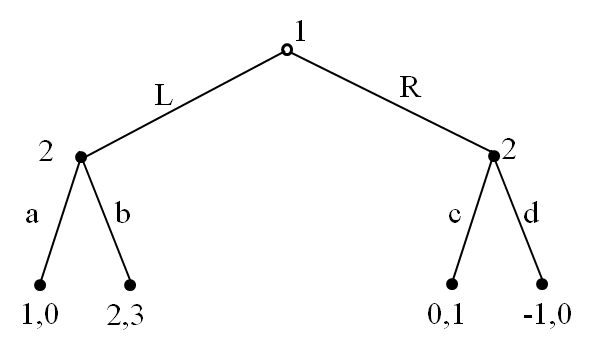
an example of Subgame
6.4.5 Subgame Perfect Equilibrium
Definition: An outcome is $a = (a_1^, a_2^, \dots, a_N^*)$ is a subgame perfect (子博弈完美) if it is a Nash Equilibrium in every subgame.
- Subgame perfect is a Nash Equilibrium.
- This definition rules out “non-credible threat”.
example
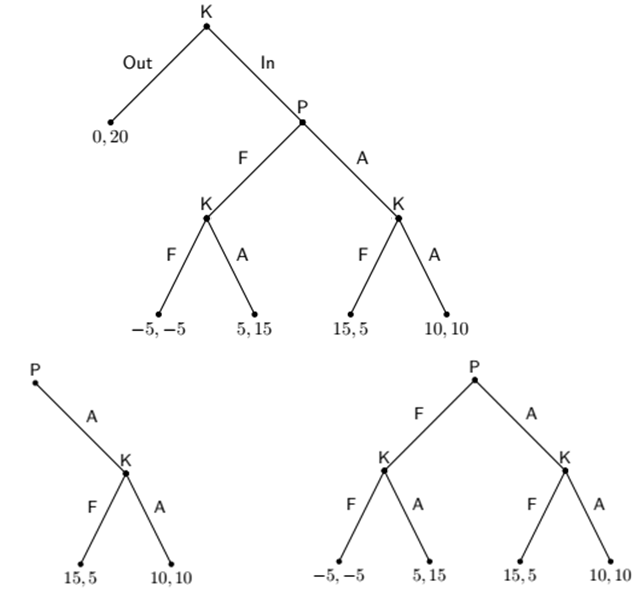
How to find Nash Equilibrium?
How to find the subgame perfect?
6.4.6 Motivation
Theorem Every extensive game with perfect information has a subgame perfect.
6.4.7 Back Induction (后向归纳)
Theorem The set of strategy game constructed by backwards induction is equivalent to the set of SPE
How to find subgame perfect Equilibria (SPE)?
Back induction is the process of “pruning the game tree” described as follows:
Step 1: start at each of the final subgame in the game, and solve for the player’s equilibrium. Remove that subgame and replace it with payoff of the player’s choice
Step 2: Repeat step 1 until we arrive at the first node in the extensive game
example
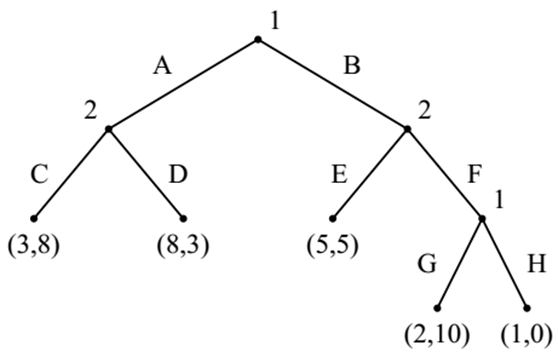
Find a Sub-game perfect Equilibrium
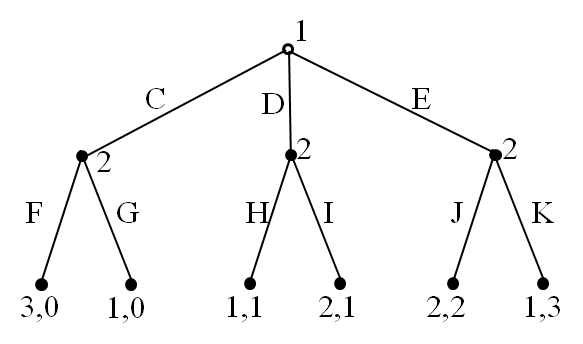
What happens for multiple optimal strategies?
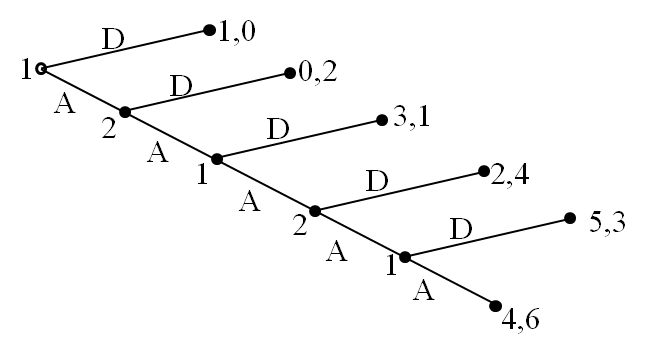
Centipede Game(蜈蚣游戏):What happens for centipede game?
最后一个节点1做选择,肯定选(5,3),2最多拿到3;倒数第二个2做选择,肯定会选择(2,4),1只能拿到2;倒数第三个1做选择,肯定会选(3,1),2只能拿到1;倒数第四个2做选择,肯定选择(0,2),1只能拿到0;第一个1肯定直接选择D(1,0)
6.5 Example
6.5.1 楼盘开发
开发商A在开发的价值8万元的楼盘时缺少3万元资金,银行B有3万元资金可以投资。 A说服B将这3万元借给自己开金矿,承诺开采到金子后与B对半分成,B是否应该将钱借给A呢?
B的忧虑: A后期是否会履行诺言?不履行承诺则需要打官司
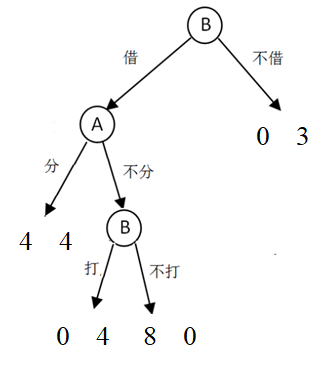
从下往上逐步分析,找到(4,4)是一个理性的结果
6.5.2 Multiple-Persons Game: Pirate Game
Five Pirates A > B > C > D > E have 1000 gold coins, and decide how to distribute them
Pirate Rules:
The most senior pirate first proposes a plan of distribution. All pirates vote on whether to accept this distribution
If the majority (including tie vote) accepts the plan, the coins are dispersed and the game ends
If the majority rejects the plan, the proposer is thrown overboard from the pirate ship and dies, and the next most senior pirate makes a new proposal to begin the system again
The process repeats until a plan is accepted or if one pirate lefts
Three decision factors
Each pirate wants to survive
Each pirate tries to maximize the number of gold coins if survival
The pirates do not trust each other, no cooperation
For D and E decisions: D: 1000 E: 0
For C, D and E decisions: C: 999 D: 0 E: 1
For B, C, D and E decisions: B: 999 C: 0 D: 1 E: 0
For A, B, C, D and E decisions: A: 998 B: 0 C: 1 D: 0 E: 1
6.6 Formal Definition of Subgame
6.6.1 Notations
Given the game $G = \{ N, H, P, \{ u_i \} \}$,
define the initial history of $h \in H$ as $A(h) = \{ a : (h, a) \in H \}$
Define the length of $G$ as $\ell(G) = \max_{h \in H} \{ |h| \}$
where $|h|$ denotes the length of the longest history in $H$.
Given a pure strategy $s_i$ and a history $h$ such that $P(h) = i$, the strategy $s_i(h) = a$ is such that $a \in A(h)$ and $a \in s_i$.
example
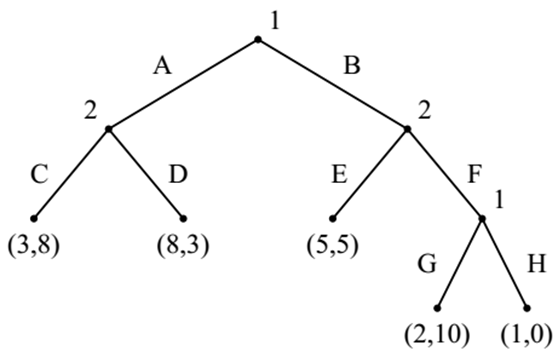
$\ell(G)=3$
$A(BF)=\{G,H\}$
$A(A)=\{C,D\}$
Given pure strategy $s_1(AG)=D$, $s_1(BF)=G$
6.6.2 Formal Definition
Given the game $G = \{ N, H, P, \{ u_i \} \}$, the subgame of the extensive game after the history $h$ is
- $H|_h$ is the set of sequences $h’ \in H$ such that $(h, h’) \in H$;
- $P|_h(h’) = P(h, h’)$ for every non-terminal history $h’ \in H|_h$;
- $u_i |_h(h’) = u_i(h, h’)$ for every terminal history $h’ \in H|_h$.
Given a pure strategy $s_i$ and history $h$,
- $s_i |_h$ is the strategy that $s_i$ induces in the subgame $G(h)$.
- $s_i |_h(h’) = s_i(h, h’)$ for every $h’ \in H|_h$.
example
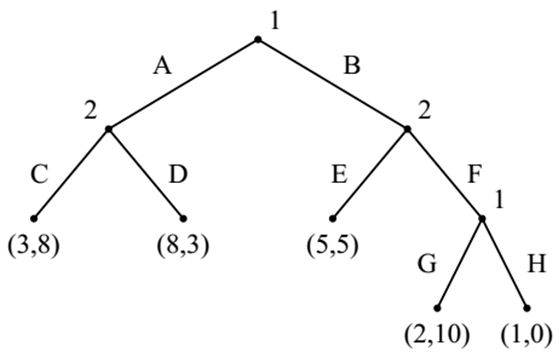
$G(B)=\{N,H|_B,P|_B,\{u_i |_B \}\}$
- $N={1,2}$
- $H|_B=\{\emptyset,E,F,FG,FH\}$
- $P|_B(\emptyset)=2,P|_B(F)=1$
- $\mu_1|_B(F,G)=2,\mu_2|_B(F,G)=10,…$
6.6.3 Subgame Perfect Equilibrium
Theorem: For a finite game $G = \{ N, H, P, \{ u_i \} \}$, a strategy profile $s^ = (s_1^, s_2^, \dots, s_N^)$ is a subgame perfect equilibrium (SPE) if and only if
for every $s_i$ in $G(h)$.
In words: $s^* |_h$ is a Nash equilibrium (NE) in every subgame $G(h)$.
6.7 One Deviation Principle (单步偏离原则)
Theorem: For a finite game $G = \{ N, H, P, \{ u_i \} \}$, a strategy profile $s^ = (s_1^, s_2^, \dots, s_N^)$ is a subgame perfect equilibrium (SPE) if and only if
for every $s_i$ in $G(h)$ that differs from $s_i^* |_h$ only in $A(h)$
$s_i(\emptyset) \neq s_i^* |_h (\emptyset)$
$s_i(h’) = s_i^* |_h (h’) \text{ for } (h, h’) \in H \text{ and } h’ \neq \emptyset$
One Deviation
Example: One Deviation Principle
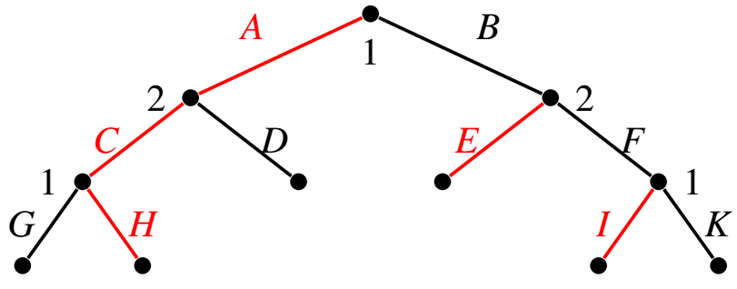
每次只偏离一步即可
Check whether (AHI,CE) is an SPE, it suffices to check
| Player 1 | Player 2 |
|---|---|
| G in the subgame G(AC) | D in G(A) |
| K in the subgame G(BF) | F in G(B) |
BHI in G, and it is not necessary to check BGK, AHK, BHK…
每次只需要更改一步即可,如:AHI去验证BHI;AHI去验证AGI;AHI去验证AHK;CE去验证DE;CE去验证CF
6.7.1 Infinite Games for One Deviation Property
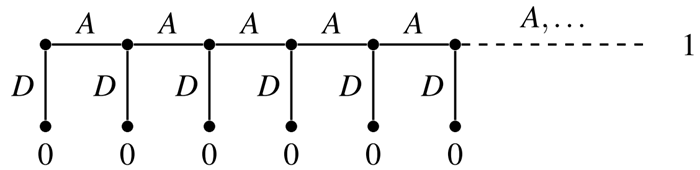
One deviation does NOT hold for infinite-length game
Strategy DDD… satisfies one-stage deviation property;AAA…is an SPE
6.8 Kuhn’s Theorem
Theorem Every finite extensive game with perfect information has a subgame perfect equilibrium.
The SPE consists of pure strategies (not mixing)
If all payoffs for each player are different, then SPE is unique
Proof is constructive and builds an SPE bottom-up (backward induction)
Finite means ‘finite length’
6.8.1 Proof
Let $G = \{ N, H, P, \{ u_i \} \}$ be a finite extensive game.
We proceed by induction on $\ell(G(h))$ for $h$.
If $\ell(G(h)) = 0$ (i.e., $h$ is a terminal history), then $R(h) = h$ is a subgame perfect equilibrium (SPE) for $G(h)$.
Now suppose $R(h)$ is defined for every $\ell(G(h)) \leq k$.
Let $h^$ be a history such that $\ell(G(h^)) = k + 1$, and let $P(h^*) = i$.
Then, $R(h^, a)$ is a SPE for every $a \in A(h^)$ since $\ell(G(h^*, a)) = k$.
Define $a^ = \max_{a \in A(h^)} \{ u_i (R(h^*, a)) \}$
Define $R(h^) = R(h^, a^*)$.
Based on the One Deviation Principle, $R(h^)$ is a SPE for $G(h^)$.
We complete the proof by setting $h^* = \emptyset$.
6.8.2 Infinite games
Kuhn’s theorem does not holds for infinite-length games
Counter example (for one player)
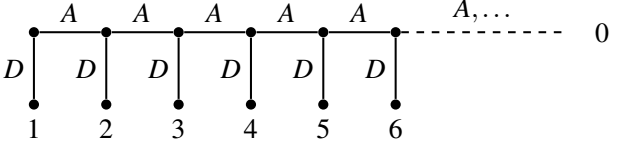
$u_1 (AAA…)=0 $
$u_1 (DDD…)=1 $
$u_1 (AAA…D…)=n+1\quad no\quad SPE$
6.9 Example
6.9.1 遗产分割问题
•姐姐先提一个分割比例,妹妹同意则按照该提议分割,若拒绝则妹妹提一个分割比例,此时遗产因通膨或官司等原因缩水一半;
•妹妹的提议,姐姐同意就按照妹妹的提议分割,若拒绝则遗产因通膨或官司等原因为零;
•假设利益相同时,两人均会接受。
问题:两姐妹如何分割遗产?
analysis
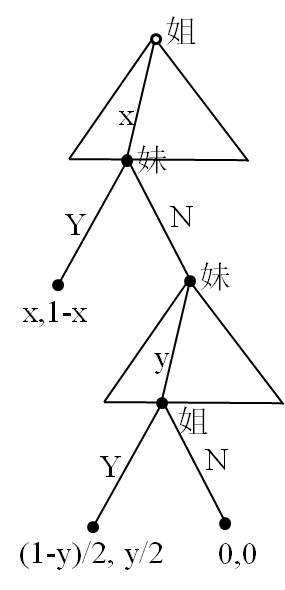
后向规划:
第二个决策阶段,姐姐接受的条件:y≥0,此时财产已缩水一半,妹妹可获得的最多比例是1/2;
第一个决策阶段,妹妹接受的最低比例:1-x ≥ 1/2,姐姐可得到的最高比例是1/2;
所以姐姐分配比例是:1/2,1/2,妹妹接受。
6.9.2 Ultimatum Game (最后通牒博弈)
The ultimatum game
Two players bargain over 1¥:
–Player 1 offers player 2 some amount 1-x≤1
–If player 2 accepts the outcome is: (x,1 - x) e.g. (0.7,0.3)
–If player 2 rejects the outcome is: (0, 0)
Each person cares about the amount of money received. Assume that x can be any scalar, not necessarily integral.
Question: What is an SPE for this game?
analysis
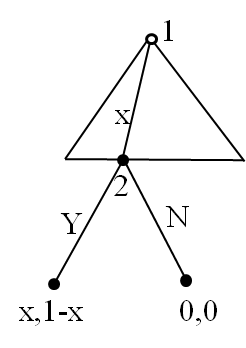
Back induction to find the SPE
Player 1’s optimal strategy
–If x<1, then accept
–If x=1, then accept or reject
If player 2 accept for any x∈[0,1]
–What is the optimal offer by player 1? x = 1
–The SPE is (1,Y)
If player 2 accept if and only if x∈[0,1)
–What is the optimal offer by A? No solution
Unique SPE (1,Y)
6.9.3 Two-Period Bargaining Game (Ultimatum Game)
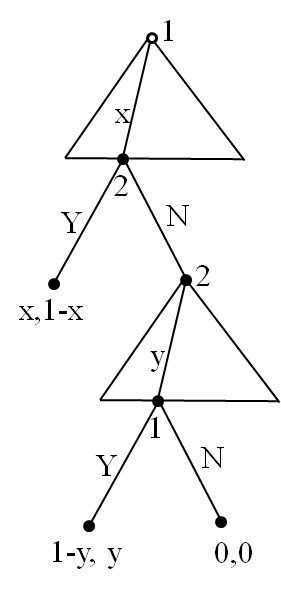
Player 1 offers player 2 some amount 1-x
Player 2 has two choices:
–Accept: (x,1-x)
–Reject: we flip the role and play again
This is the second period of the game
The second period is an ultimatum game:
-Player 2 offers player 1 some amount 1-y
-If player 1 accepts, the deal is done
-If player 1 rejects, none of them gets anything
Discount Factor
We add one important factor
–In the first round, the pie is worth 1¥
–If we end up in the second round, the pie is worth less
Example:
–If I give you 1¥ today, that’s what you get
–If I give you 1¥ in 1 year, we assume it’s worth less, say δ<1
Discounting factor:
–From today perspective, 1¥ tomorrow is worth δ<1
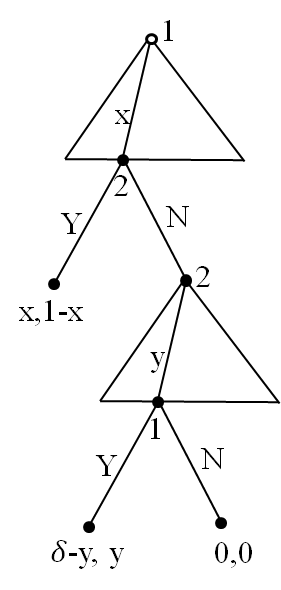
Backward induction:
- The unique SPE in the second period (0,δ)
- What you should offer in the first period: player 1 offer x=1-δ
| Player 1 | Player 2 | |
|---|---|---|
| 1-period | 1 | 0 |
| 2-period | 1-δ | δ |
In the second round of the two-period game, player 2 gets the whole pie
The pie in the second round, that player 2 gets, is worth less than 1¥
6.9.4 Three-Period Bargaining Game
The rules are the same as for the previous games, but now there are two possible flips:
- Period 1: player 1 offers first
- Period 2: if player 2 rejected in period 1, she gets to offer
- Period 3: if player 1 rejected in period 2, he gets to offer again
Discounting factor:
−the value of a pie in round three is discounted by $δ$
−the value of a pie in round three is discounted by $δ^2$
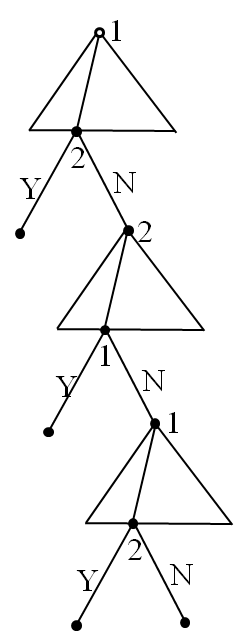
In the third round
–Unique SPE $(δ^2,Y)$
–Payoffs $(δ^2,0)$
In the second round
–Unique SPE $(δ-δ^2,Y)$
–payoffs$ (δ^2,δ-δ^2)$
In the first round
–Unique SPE $(1-δ+δ^2,Y)$
–payoffs $(1-δ+δ^2,δ-δ^2)$
| Player 1 | Player 2 | |
|---|---|---|
| 1-period | 1 | 0 |
| 2-period | 1-δ | δ |
| 3-period | 1-δ(1-δ) | δ(1-δ) |
In the second round of the two-period game, player 2 gets the whole pie
The pie in the second round, that player 2 gets, is worth less than 1¥
6.9.5 Result for Four-Period Bargaining Game
| Player 1 | Player 2 | |
|---|---|---|
| 1-period | 1 | 0 |
| 2-period | 1-δ | δ |
| 3-period | 1-δ(1-δ) | δ(1-δ) |
| 4-period | ? | ? |
Large Number of Period Bargaining Game
Geometric series
payoff for player 1 on n-period bargaining
$1-δ+δ^2-δ^3+…+(-δ)^{n-1}=\frac{1-(-δ)^n}{1+δ}$
payoff for player 2 on n-period bargaining
$1-\frac{1-(-δ)^n}{1+δ}=\frac{δ-(-δ)^n}{1+δ}$
Let’s look at the asymptotic behavior of this game, when there is an infinite number of stages
Player 1: $\frac{1-(-δ)^n}{1+δ}→ 1/(1+δ)$
Player 2: $\frac{δ-(-δ)^n}{1+δ} → δ/(1+δ)$
Let’s imagine that the offers are made in rapid succession: this would imply that the discount factor we hinted at is almost negligible $δ→1$
So, if we assume rapidly alternating offers, we end up with a 0.5-0.5 split!