[TOC]
8.1 Supplements for Nash Equilibrium
Player 1: $P_1 = (p_{11}, p_{12})$
Payoff for Player 1: $U_1 = P_1 L P_2^\top$
Player 2: $P_1 = (p_{21}, p_{22})$
Payoff for Player 2: $U_1 = P_1R P_2^\top$
8.1.1 NE
$
\text{Two players with payoff matrices } L \text{ and } R \text{ of size } m \times n
$
$
P_1 = (p_{11}, p_{12}, \dots, p_{1m})
$
$
P_2 = (p_{21}, p_{22}, \dots, p_{2n})
$
$
(P_1, P_2) \text{ is a Nash equilibrium (NE) if and only if }
$
$
P_1 L P_2^\top \geq P_1’ L P_2^\top \text{ for all mixed strategies } P_1’
$
$P_1 R P_2^\top \geq P_1 R [P_2’]^\top \text{ for all mixed strategies } P_2’$
或者可以这么说:
$
(P_1, P_2) \text{ is a NE if and only if}
$
$
P_1 L P_2^\top \geq e_i L P_2^\top \text{ for every } i \in [m] \quad e_i = (0, \dots, 0, 1, 0, \dots, 0)
$
$
P_1 R P_2^\top \geq P_1 R e_i^\top \text{ for every } i \in [n] \quad e_i = (0, \dots, 0, 1, 0, \dots, 0)
$
8.1.2 Strategy game
$
\text{Player 1’s mixed strategy: } \mathbf{x} = (x_1, 1 - x_1)
$
$
\text{Player 2’s mixed strategy: } \mathbf{y} = (y_1, 1 - y_1)
$
$
\text{Player 1’s payoff: } \mathbf{x} L \mathbf{y}^\top
$
$
\text{Player 2’s payoff: } \mathbf{x} R \mathbf{y}^\top
$
8.2 Stackelberg game (主从博弈)
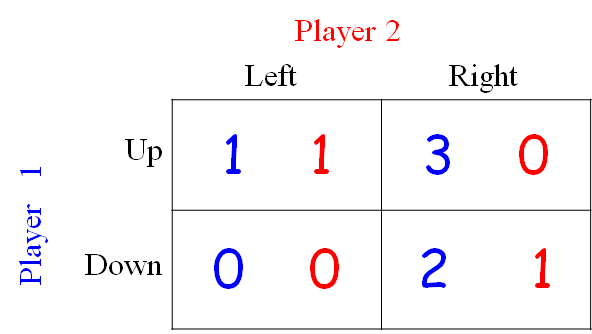
Player 1: “leader” Player 2 “follower”
1) Leader selects a (possibly mixed) strategy $x_1$
2) Follower learns about $x_1$, selects the best response $x_2$
8.2.1 如何表示主从博弈
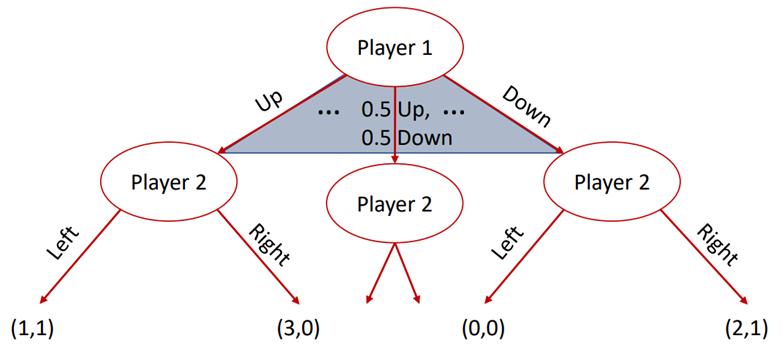
Mixed strategies are hard to visually represent
- Continuous spectrum of possible actions
- 行动的连续谱
8.2.2 主从博弈的纳什均衡
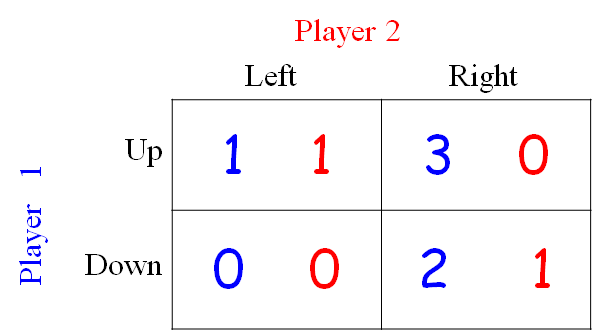
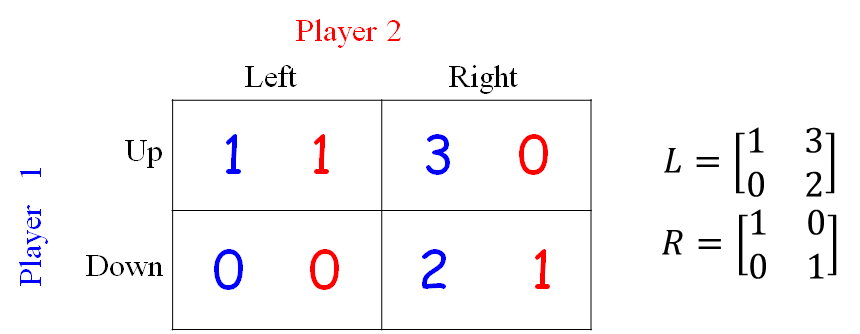
Player 1 takes mixed strategies, the advantage is more:
- If Player 1 plays Up and Down with probabilities 0.49 and 0.51, respectively
- Player 2 is still better off playing Right than Left, in expectation
- The Reward of Player 1 >2
Can the leader lose in Stackelberg equilibrium compared to a Nash equilibrium?
- In Stackelberg, the leader must take action in advance, while in Nash, he can change his strategy at any point.
- The answer: No
- The optimal reward for the leader in the Stackelberg game is always greater than or equal to his maximum reward under any Nash equilibrium.
- If (x,y) is a NE, then Player 1 can always select x, ensure that Player 2 will play y and achieve the reward in NE
- Player 1 may be able to select a better strategy than x
- 后选择的总是被动
8.2.3 Stackelberg vs Nash
It is important to note that:
- the leader can take mixed strategies
- the follower knows (and trusts) the leader’s strategies
- the leader knows the follower’s reward structure
8.3 Stackelberg in zero-sum game
Recall the minimax theorem:
Player 1 goes first $\rightarrow$ Player 1 selects the maxmin strategy.
Player 2 goes first $\rightarrow$ Player 2 selects the minmax strategy.
The minimax theorem: make no difference.
Strategy game and Stackelberg game in zero-sum are essentially identical.
策略博弈和零和中的斯塔克伯格博弈本质上是相同的。
Proof:
- $U_{1st}\geq U_{1NE}$
- $U_{2st}\geq U_{2NE}$
- $-U_{1st}\geq U_{2NE}=-U_{1NE}$
- $U_{1st}\leq U_{1NE}$
- $U_{1st}=U_{1NE}$
8.3.1 Stackelberg for general 2-persons game
2-persons game: the payoff matrices are L and R for player 1 and 2, respectively.
8.3.2 example
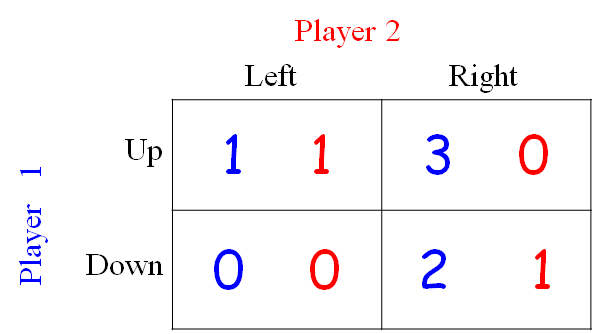
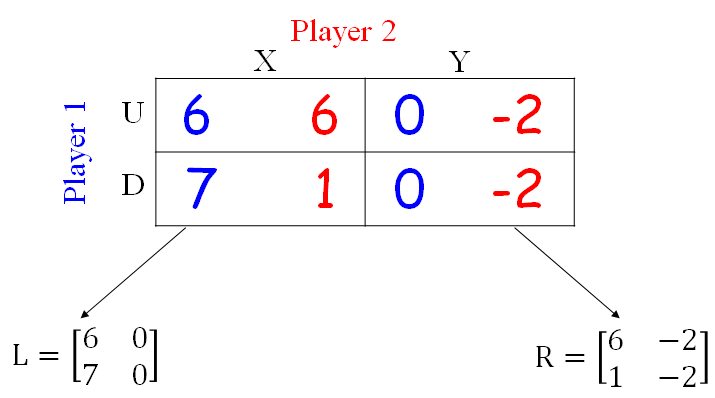
Mixed strategy x=(p,1-p) over ‘Up’ and ‘Down’. Consider two cases:
- Player 2 selects ‘Left’
- Player 2 selects ‘Right’
case 1
Player 2 selects ‘Left’ :
$\max_{p \in [0, 1]} \left( 1p + 0(1 - p) \right)$
subject to $p \cdot 1 + 0 \cdot (1 - p) \geq 0 \cdot p + 1 \cdot (1 - p)$
That is:
$\max_{p \in [0, 1]} p$
subject to : $p \geq 1 - p$
Solution : p=1,the payoff : 1
case 2
Player 2 selects ‘Right’ :
$\max_{p \in [0, 1]} \left( 3p + 2(1 - p) \right)$
subject to : $p \cdot 1 + 0 \cdot (1 - p) \leq 0 \cdot p + 1 \cdot (1 - p)$
That is:
$\max_{p \in [0, 1]} \left( p + 2 \right)$
subject to : $p \leq 1 - p$
Solution : p=1/2,the payoff : 2.5
8.3.3 Stackelberg via linear programs
High-level idea:
- Fix a strategy $ a_2^* \in A_2 $ for Player 2.
- Write a linear program with mixed strategy $\mathbf{x}$ of Player 1.
- Maximize the payoff of Player 1 with respect to mixed strategy $\mathbf{x} $, and Player 2 selects the best response $ a_2^* $.
- Solve this linear program.
Solve linear programs for every $ a_2^* \in A_2 $.
8.3.4 Stackelberg via linear programs (formally)
$A$, $B$ for player 1 (Leader) and player 2 (Follower)
$|A| = m$, $|B| = n$
$\mathbf{x}$ is a mixed strategy over $A$
$\mathbf{x}(a_i)$ denotes the probability of Leader selecting $a_i \in A$
$u_1(a, b)$ and $u_2(a, b)$: payoff for Leader and Follower
One LP for fixed $ b^* \in A_2 $
Fixed strategy $ b^* \in A_2 $ for player 2 (Follower)
$U_1(b^) = \max \sum_{a \in A} \mathbf{x}(a) u_1(a, b^)$
subject to
- $\forall b \in B, \sum_{a \in A} \mathbf{x}(a) u_2(a, b^*) \geq \sum_{a \in A} \mathbf{x}(a) u_2(a, b)$
- $\sum_{a \in A} \mathbf{x}(a) = 1, \quad \mathbf{x}(a) \geq 0$
Taking the maximum over $b \in A_2 $ : $\max_{b} U_1(b)$
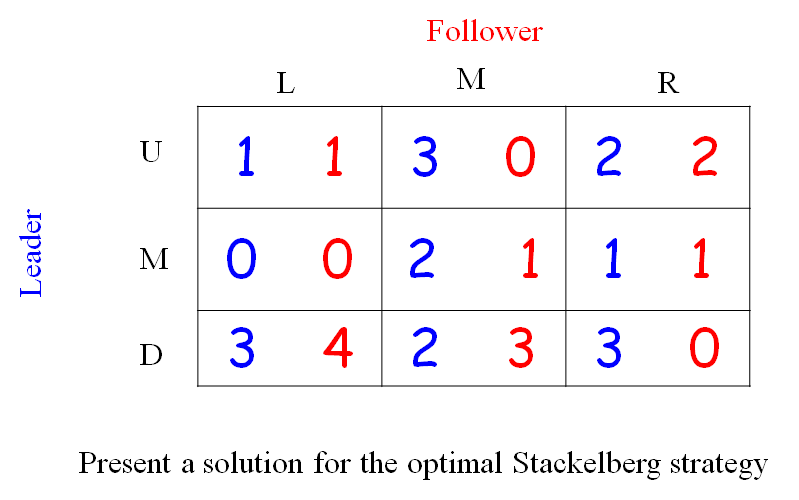
exercise

2选择Left
结果:$[\frac{1}{3},0,\frac{7}{3}]$,payoff:$\frac{7}{3}$
2选择middle
结果:$[\frac{3}{5},\frac{2}{5},0]$,payoff:$\frac{11}{5}$
2选择right
结果:$[\frac{1}{3},0,\frac{2}{3}]$,payoff:$1$
因此选择left有最大收益$\frac{7}{3}$
- 上面的s.t.指的是在follower有这种选择必须满足的条件:即当前选择的利好必须不小于其他的选择
8.4 Computing Stackelberg
Theorem [Conitzer and Sandholm 2006]: In 2-player normal form games, an optimal Stackelberg strategy can be found in polynomial time.
Theorem: In (>)3-player normal form games, an optimal Stackelberg strategy is an NP-Hard problem.
8.5 Cournot Competition (Strategy game)
Two firms compete by choosing how much to produce:
$G = \{ {1, 2}, {q_1, q_2}, {u_1, u_2} \}$
价格函数为:$p(q_1 + q_2) = \max \left( 0, a - b(q_1 + q_2) \right)$
公司的成本函数为:$c_i(q_i) = c q_i$
收益函数为:$u_i(q_1, q_2) = \left( \max \left( 0, a - b(q_1 + q_2) \right) - c \right) q_i$
条件为:$a > b, , c > 0, , q_1 \geq 0, , q_2 \geq 0$
纳什均衡为:$\left( \frac{a - c}{3b}, \frac{a - c}{3b} \right)$
8.5.1 Stackelberg Competition (主从博弈)
Here’s the version you requested in LaTeX format with the modifications made:
$G = \{ {1, 2}, {q_1, q_2}, {u_1, u_2} \}$
The price function is:$p(q_1 + q_2) = \max \left( 0, a - b(q_1 + q_2) \right)$
The cost functions for the firms are: $c_i(q_i) = c q_i$
The payoff functions are: $u_i(q_1, q_2) = \left( \max \left( 0, a - b(q_1 + q_2) \right) - c \right) q_i$
The conditions are: $a > b, , c > 0, , q_1 \geq 0, , q_2 \geq 0$
Difference: Player 1 chooses $q_1$ first, then Player 2 chooses $q_2$ after observing $q_1$.
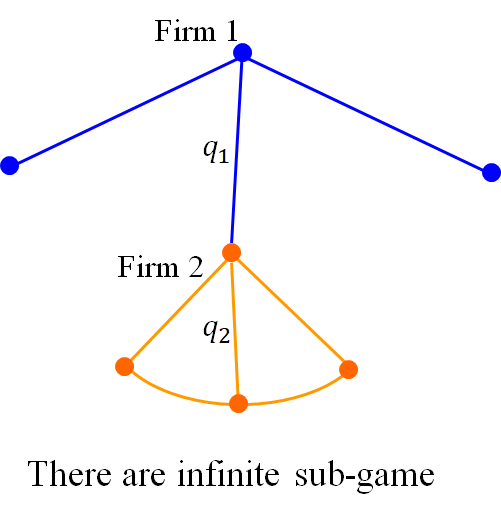
8.5.2 Stackelberg Competition (Continued)
This is an extensive game, and we look for Subgame Perfect Equilibrium (SPE).
Back Induction – Not a finite game but with finite length.
We look at a subgame where player 1 chooses $q_1$. Then, player 2 ’s maximization problem is:
This gives the best response for player 2:
No difference.
8.5.3 Stackelberg Competition (Continued)
The difference: Player 1 will choose $q_1$ after recognizing player 2 ’s best response. Player 1 is the leader; player 2 is the follower.
The problem for player 1 is:
subject to
This implies that:
We get the best response for player 1:
This gives the best response for player 2:
SPE: Player 1 has an advantage.
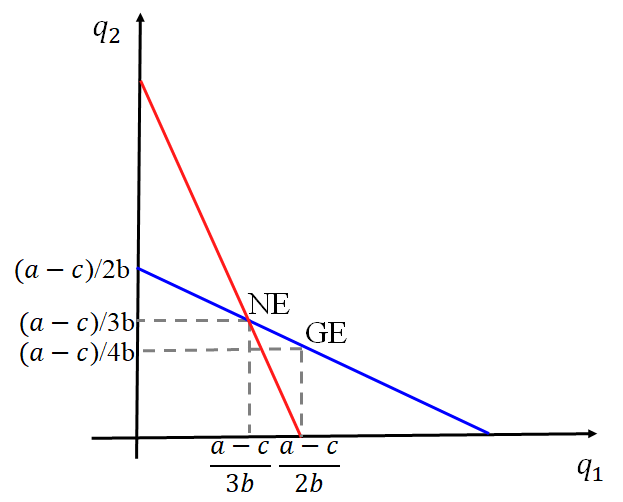
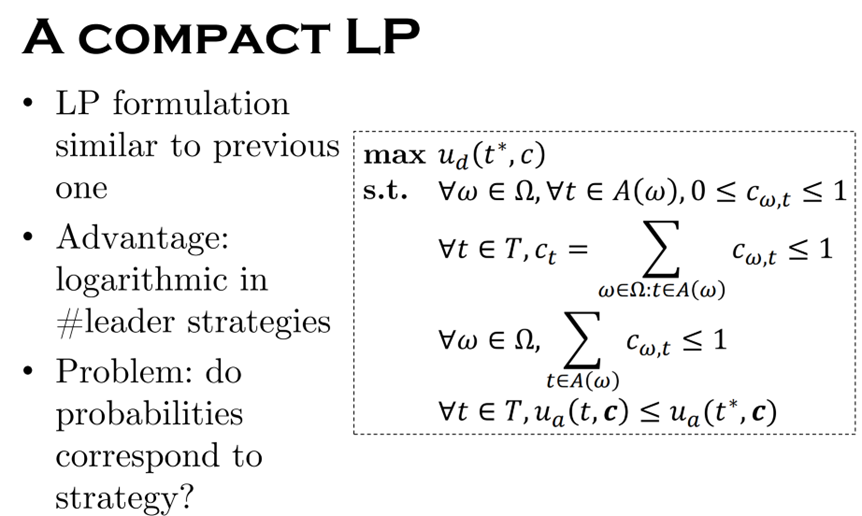
8.6 Real-world Applications*
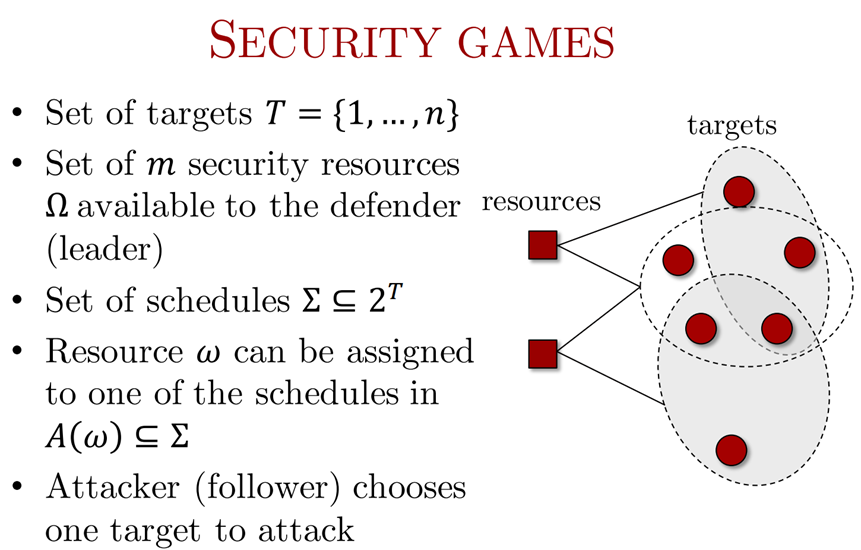
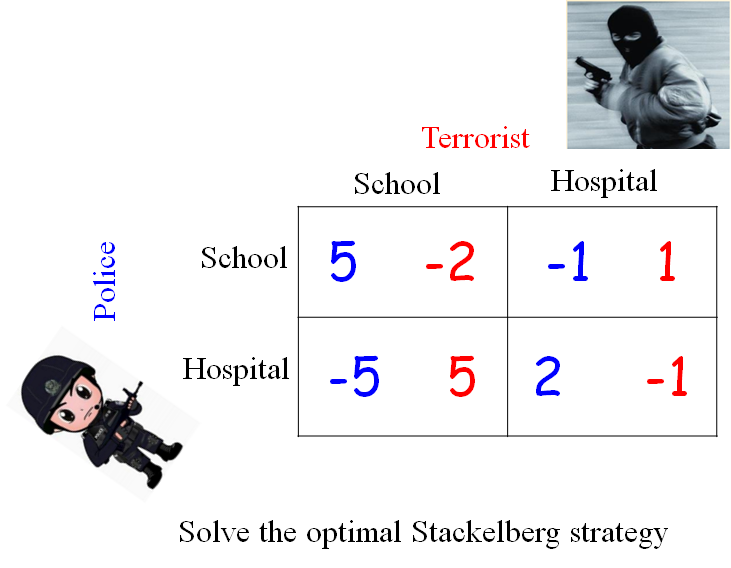
8.6.1 Security Game
Security Game: Defender selects a mixed strategy; attacker follows by choosing a target to attack.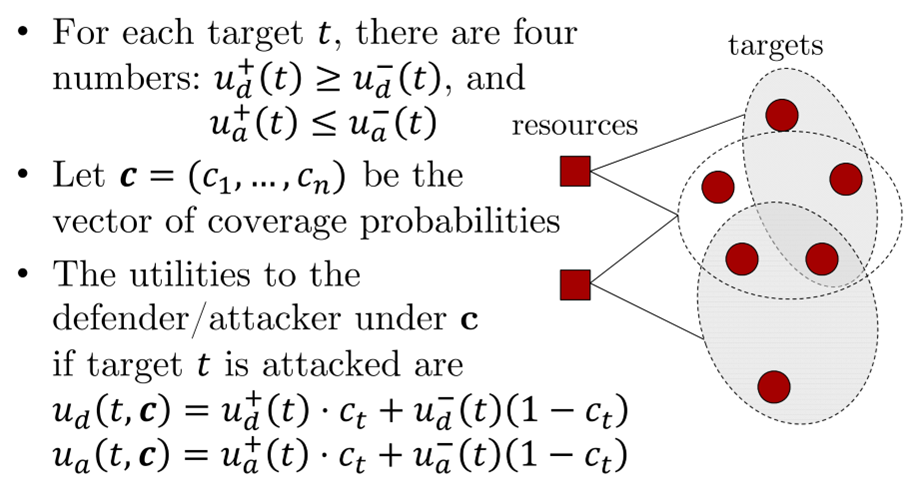

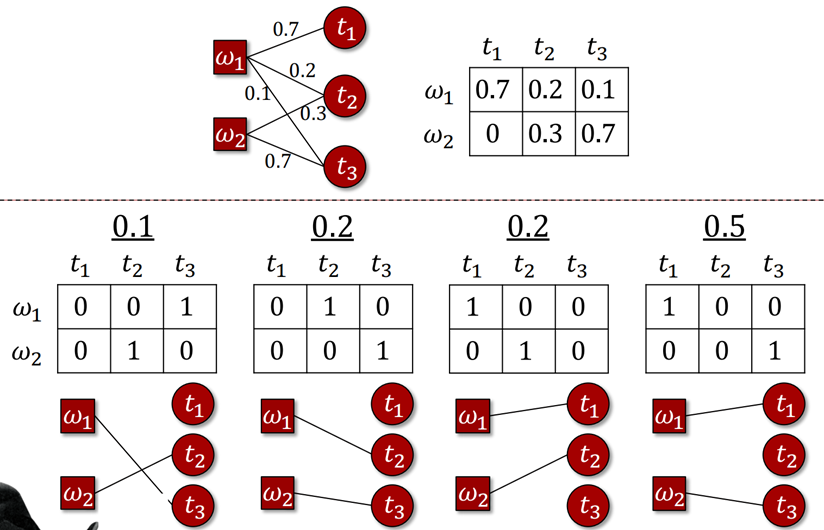
8.6.2 example
8.6.3 homework