第十章 Extensive Game with Imperfect Information

10.1 Motivation 动机

Extensive game with perfect information

• Know all previous strategies for all players

Sometimes, players

• Don’t know all the strategies the other take or

  不知道其他人的策略

  

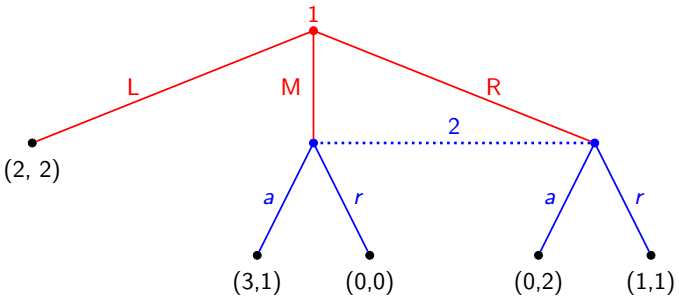
  Player 2 does not know the choice of player 1 over M or R

• Don’t recall all their own past actions

  记不清自己之前是否做过策略

  

  Player 1 does not know if he has made a choice or not

Extensive game captures some of this unknown

• A later choice is made without knowledge of an earlier choice

How to represent the case two players make choices at the same time, in mutual ignorance of each other

上面的两种形式的详细说明：

1. 贝叶斯博弈（Bayesian Game）：
   • 在这种形式的博弈中，玩家并不知道其他玩家的确切行动，而是基于概率分布（信念）对其他玩家的状态或类型进行推测。
   • 玩家根据他们的信念选择策略，而不是完全的确定性信息。每个玩家在做出决策时会考虑到其他玩家可能的行动和类型。
2. 信息集博弈（Information Set Game）：
   • 在这种形式的博弈中，玩家在某些决策节点上无法区分自己所处的历史路径，这些决策节点构成了玩家的信息集（information set）。
   • 每个信息集包含多个可能的历史节点，玩家只知道自己所处的某个信息集，但无法得知更具体的历史（例如，哪些行动已经被其他玩家采取）。
   • 玩家只能基于他们的当前信息集来选择策略。

10.2 Definition of extensive game with Perfect Information

An extensive game with perfect information is defined by $G = \{ N, H, P, \{ u_i \} \}$, where:

• Players $N$ is the set of $N$ players
• Histories $H$ is a set of sequence $a^1, a^2, \dots, a^k$, with each component $a^i$ is a strategy
• Player function $P(h): H \to N$ is the player who takes action after history $h$,
• $u_i$ is the payoff function for player $i$,
• $A(h) = \{ a : (h, a) \in H \}$ is the set of available actions at a non-terminal history $h$.

10.2.1 Ultimatum Game 最终通牒博弈

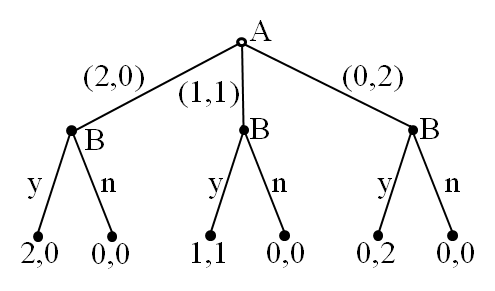
$G = \{ N, H, P, \{ u_i \} \}$

$N = \{ A, B \}$, where $A$ and $B$ are the two players.

$H = \{\emptyset, (2, 0), (1, 1), (0, 2), ((2, 0), y), ((2, 0), n), ((1, 1), y), ((1, 1), n), ((0, 2), y), ((0, 2), n)\}$ is the set of histories:

The player function $P$ is defined as:

• $P(\emptyset) = A$, meaning Player A moves first.
• $P((2, 0)) = B$, $P((1, 1)) = B$, $P((0, 2)) = B$, meaning Player B moves after the corresponding histories.

The action set $A$ is defined as:

• $A(\emptyset) = \{(2, 0), (0, 2), (1, 1)\}$, the set of possible actions Player A can take from the starting point.
• $A((2, 0)) = A((0, 2)) = A((1, 1)) = \{ y, n \}$, the set of possible actions Player A can take after each of the respective histories.

10.2.2 Extensive Game with Imperfect Information

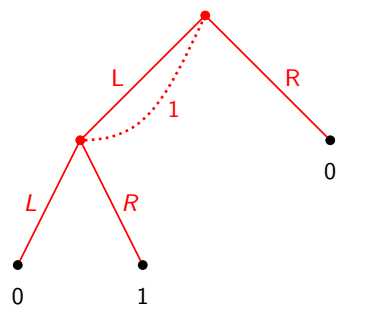
Player 1 does not know the choice of player 2 over LA or LB

Nonterminal histories:$ \{∅,L,LA,LB\} $

• Player 1 has information set $I_1=\{∅,\{LA,LB\}\}$

• Player 2 has information set $I_2=\{\{L\}\}$

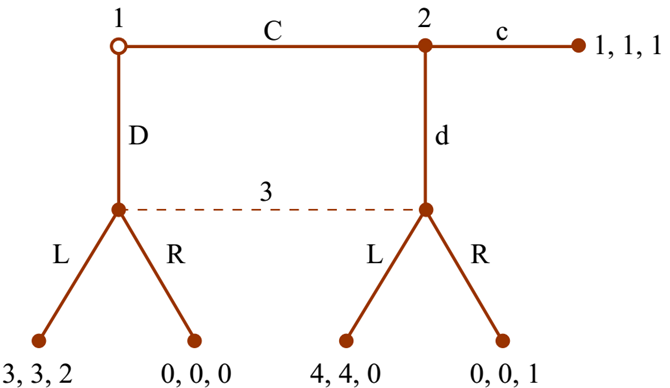
• Player 1 has the information set $I_{11} = \{\emptyset\}$.
• Player 2 has the information set $I_{21} = \{C\}$.
• Player 3 has the information set $I_{31} = \{D, Cd\}$.

10.3 Definition of Extensive Game with Imperfect Information

An extensive game with imperfect information is defined by $G = \{ N, H, P, I, \{ u_i \} \}$.

• Information set $I = \{ I_1, I_2, \dots, I_N \}$ is the set of information partitions of all players’ strategy nodes, where the nodes in an information set are indistinguishable to the player.

  $I_i = \{ I_{i1}, \dots, I_{ik_i} \}$ is the information partition of player $i$.

  玩家$i$的所有信息集的集合，表示该玩家能够区分或无法区分的历史节点的分组。每个信息集内的节点对于玩家$i$来说是无法区分的。

  $I_{i1} \cup \dots \cup I_{ik_i} = \text{all nodes of player } i$.

  $I_{ij} \cap I_{ik} = \emptyset$ for all $j \neq k$.

  Action set $A(h) = A(h’)$ for $h, h’ \in I_{ij}$, denoted by $A(I_{ij})$.

  $P(I_{ij})$ is the player who plays at information set $I_{ij}$.

An extensive game with perfect information is a special case where each $I_{ij}$ contains only one node. 即完美信息博弈的时候：每个信息集$ I_{ij} $只包含一个节点，即玩家在任何时刻都可以完全了解所有之前的历史

10.4 Pure Strategies

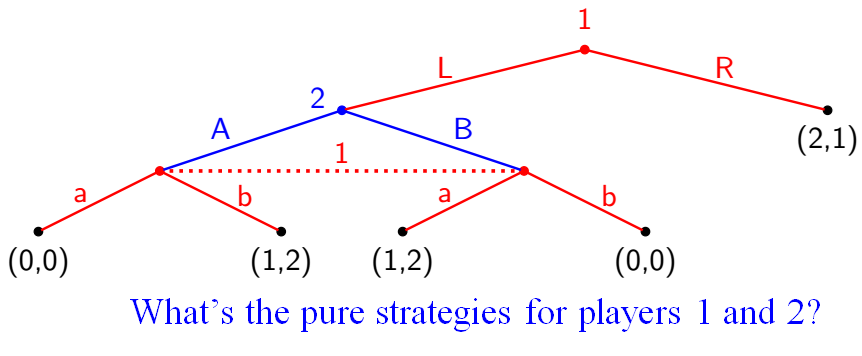
A pure strategy for player $i$ selects an available action at each of player $i$’s information sets $I_{i1}, \dots, I_{im}$.

All pure strategies for player $i$ are:

$$A(I_{i1}) \times A(I_{i2}) \times \dots \times A(I_{im})$$

where $A(I_{ij})$ denotes the strategies available in the information set $I_{ij}$.

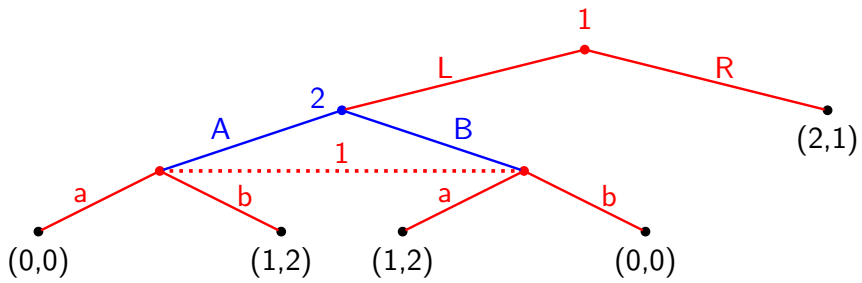
• $I_1 = \{ I_{11}, I_{12} \} = \{\emptyset, \{ LA, LB \} \}$
• $I_2 = \{ I_{21} \} = \{ L \}$
• $A(I_{21}) = \{ A, B \}$
• The pure strategy for player 2: $A$, $B$.
• $A(I_{11}) = \{ L, R \}$, $A(I_{12}) = \{ a, b \}$
• The pure strategy for player 1: $La$, $Lb$, $Ra$, $Rb$.

10.5 Normal-Form Representation of Extensive Imperf. Game

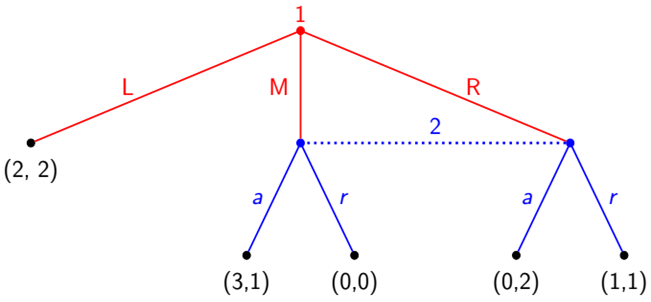
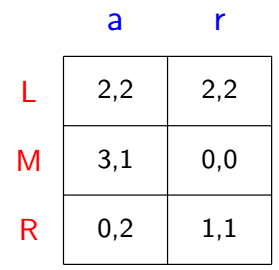
The pure and mixed strategy Nash Equilibrium remains?

What’s the difference from the extensive game with perfect information game?

10.5.1 A strategy game $\rightarrow$ An extensive game with imperfect inf.

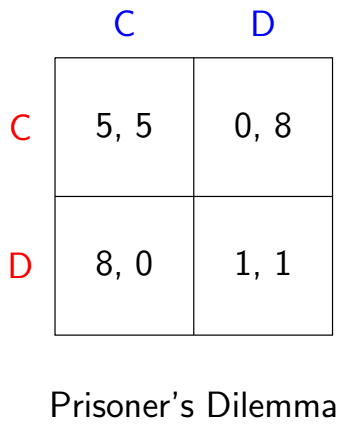
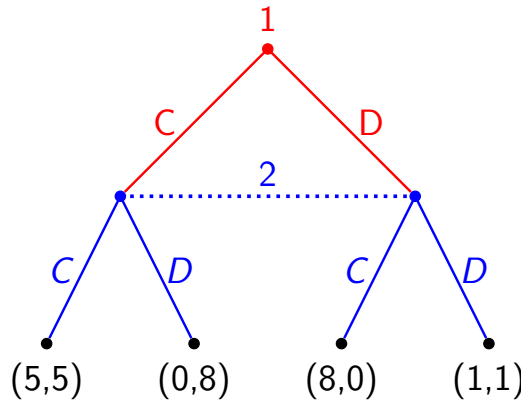
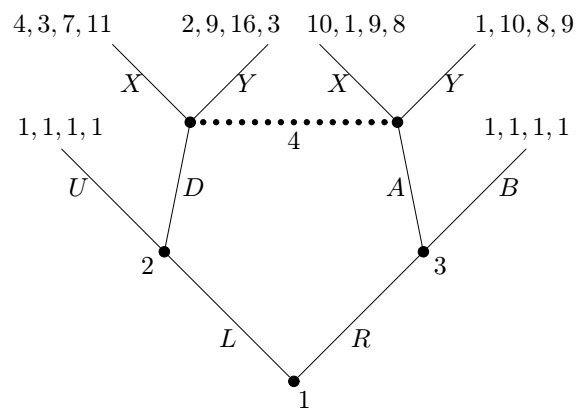
10.5.2 Exercise: 3-Players Game

10.6 Perfect Recall (完美回忆) and Imperfect Recall

An extensive game has perfect information if each information set consist of only one nodes

An extensive game has perfect recall if each player recalls exactly what he did in the past

• otherwise, this game has imperfect recall

10.6.1 example

Perfect recall

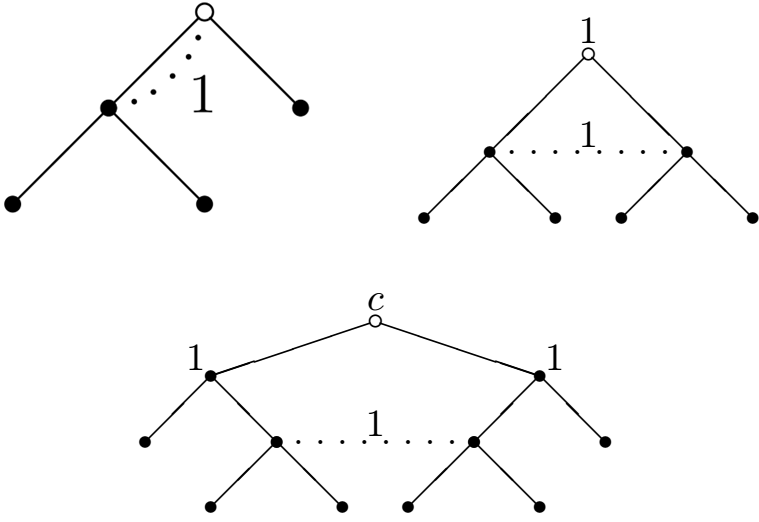
Imperfect recall

10.6.2 Formal Definition of Perfect Recall

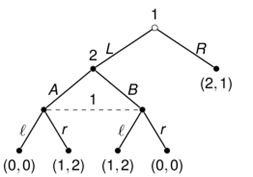
Definition (Experience record): Given a history $h$ of an extensive game, the function $X_i(h)$ is the sequence consisting of information sets that player $i$ encounters in $h$ and the actions that player $i$ takes at them. $X_i$ is called the experience record of player $i$ in $h$.

经验记录是一个函数，记作 $X_i(h)$，其中：

• h是某个特定的历史（即游戏的某个状态或节点）。
• $X_i(h) $是一个序列，包含了玩家 i在历史 h所遇到的所有信息集，以及玩家 i在这些信息集中的所做的选择。

经验记录的关键在于，信息集代表的是玩家对历史节点的“感知”。在不完全信息博弈中，同一个信息集中的所有节点对该玩家来说是无法区分的，玩家无法知道他所处的具体节点，只能知道他所处的某个信息集。

Example: In our example game, Player 1 encounters two information sets in the history $h = LA$, namely $\emptyset$ and $\{ LA, LB \}$. In the first information set, he chooses $L$. So, the experience record for player 1 is: $ X_1(h) = \{\emptyset, L, \{ LA, LB \} \} $.

Definition (Perfect Recall): An extensive game has perfect recall if for each player $i$, we have $X_i(h) = X_i(h’)$ whenever the histories $h$ and $ h’$ are in the same information set of player i.

完美记忆（Perfect Recall）的定义：在一个扩展博弈中，如果对于每个玩家 $i$，在同一信息集中的两个历史 $h$ 和 $h’$，都有 $X_i(h) = X_i(h’)$，那么这个博弈就被称为具有完美记忆。也就是说，如果玩家 $i$ 认为某两个历史是无法区分的（即它们属于同一个信息集），那么在这两个历史下，玩家的经验记录应当是相同的。

Example: In our example game, the only non-singleton information set satisfies the condition, since for $h = LA$ and $h’ = LB$ we have
$X_1(h) = X_1(h’) = \{\emptyset, L, \{ LA, LB \}\}. $ For the imperfect recall examples, the actions are different for the two histories ending up in the non-singleton information set.

这两个同一信息集中的LA和LB的记忆记录相同，因此是完美回忆

10.7 Definition of Mixed and Behavioral Strategies

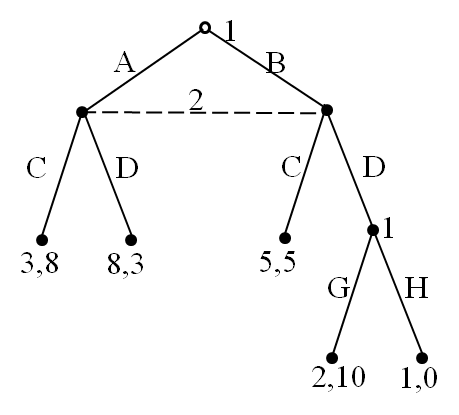
Mixed Strategies: A mixed strategy of player i in an extensive game is a probability over the set of player i’s pure strategy

Behavioral strategies: A behavioral strategy of player $i$ is a collection $\beta_{ik}(I_{ik})$ for each $I_{ik} \in I_i$ of independent probability measures, where $\beta_{ik}(I_{ik})$ is a probability measure over $A(I_{ik})$.

行为策略：在每个信息集中做的决策，每个决策通过独立的概率分布来确定

Behavioral strategies distinguish from mixed strategies：

A behavioral strategy for player 1:

• Selects A with prob. 0.5, and B otherwise

• choose G with prob. 0.3, and H otherwise

Here’s a mixed strategy that isn’t a behavioral strategy

• Pure Strategy AG with probability 0.6, pure strategy BH 0.4

• The choices at the two nodes are not independent

区别就是是否独立的问题

行为策略与混合策略的主要区别在于，行为策略是在每个信息集内进行概率选择的，而不是选择整场游戏中的某个纯策略

10.7.1 Behavioral vs. Mixed Strategies

In imperfect-information games, mixed and behavioral strategies produce different sets of equilibria

• In some games, mixed strategies can achieve equilibria that aren’t achievable by any behavioral strategy
• In some games, behavioral strategies can achieve equilibria that aren’t achievable by any mixed strategy

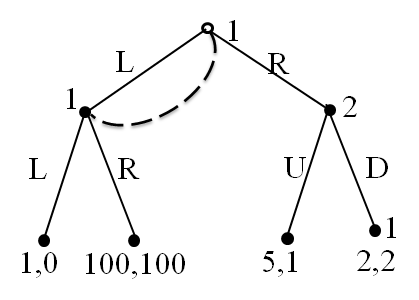
Consider game

• Player 1 inform. set: $\{\{\emptyset, L\}\}$

Player 1: R is a strictly dominant strategy

因为不知道之前有没有做过决策，如果选择L可能直接获得1，但是选择R至少获得2

还是没有完全理解这两者之间的关系

Player 2: D is a strictly dominant strategy

• (R, D) is the unique Nash equilibrium for mixed strategy

1: the information set is {(∅,L)}

2: D is a strictly dominant strategy

Player 1’ s best response to D:

• Player 1’ s the behavioral strategy [L, p;R, 1 - p] i.e., choose L with probability p

• The expected payoff of player 1 is

• $U_1=p^2+100p(1 - p)+2(1-p)=-99p^2+98p+2$

• To find the maximum, we have p=49/99

(R,D) is not an equilibrium for behavioral strategy

10.7.2 Kuhn Theorem (1953)

Theorem In an finite extensive game with perfect recall

• any mixed strategy of a player can be replaced by an equivalent behavioral strategy

• any behavioral strategy can be replaced by an equivalent mixed strategy

• Two strategies are equivalent

Corollary In an finite extensive game with perfect recall, the set of Nash equilibrium does not change if we restrict ourselves to behavior strategies

在完美信息博弈上这二者等同

10.7.3 example

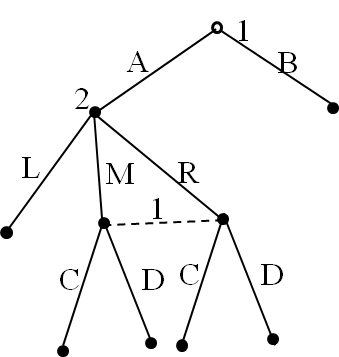
What behavioral strategy is equivalent to mixed strategy $(p_{AC},p_{AD}, p_{BC}, p_{BD})$

•$I_{11}=\{∅\}; I_{12}=\{AM,AR\}$

•$A(I_{11} )=\{A,B\}$

•$A(I_{12} )=\{C,D\}$

$$\beta_{11} (I_{11})(A) = p_{AC} + p_{AD}, \quad \beta_{11} (I_{11})(B) = p_{BC} + p_{BD}$$ $$\beta_{12} (I_{12})(C) = \frac{p_{AC}}{p_{AC} + p_{AD}}, \quad \beta_{12} (I_{12})(D) = \frac{p_{AD}}{p_{AC} + p_{AD}}$$

What mixed strategy is equivalent to behavioral strategy of prob. p over A and q over C

$$(p_{AC}, p_{AD}, p_{BC}, p_{BD}) = (pq, p(1 - q), (1 - p)q, (1 - p)(1 - q))$$

10.8 Extensive Imperfect Subgame

Definition A subgame of an extensive imperfect game G is some node in the tree G and all the nodes that follow it, with the properties that any information set of G is either completely in or outside the subgame

对于博弈树中的每个信息集，它要么完全包含在子博弈中，要么完全不包含在子博弈中，这确保了子博弈的结构是连贯的，且不涉及在子博弈之外的历史信息

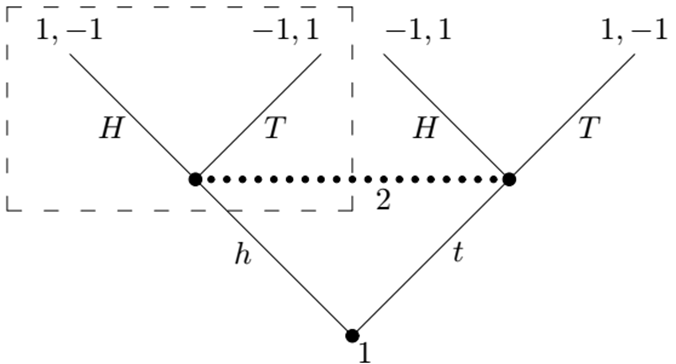
Definition A subgame perfect Nash equilibrium of an extensive form game G with perfect recall is a outcome of behavior strategies $(β_1, β_2,…,β_N)$ such that it is a Nash Equilibrium for every subgame

Theorem Every finite extensive game with perfect recall has at least one subgame perfect Nash Equilibrium

10.8.1 example

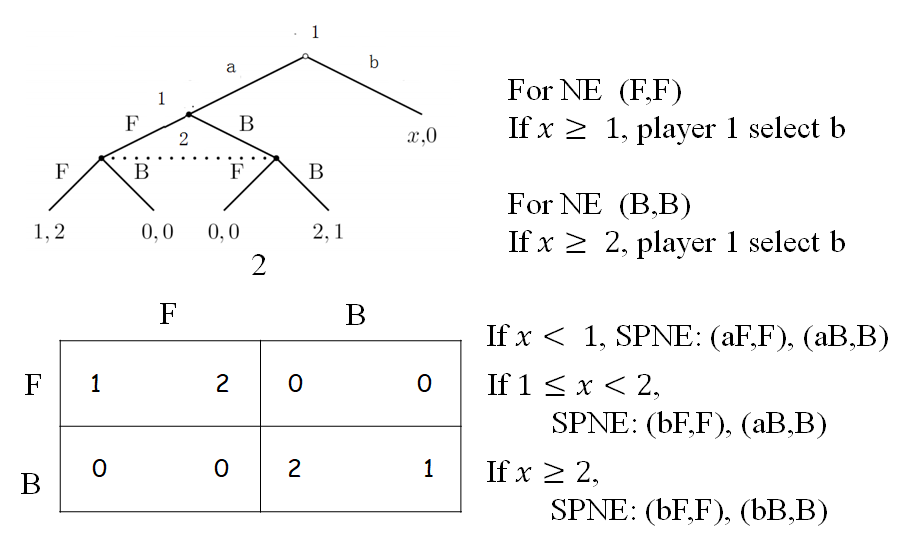
10.9 Belief

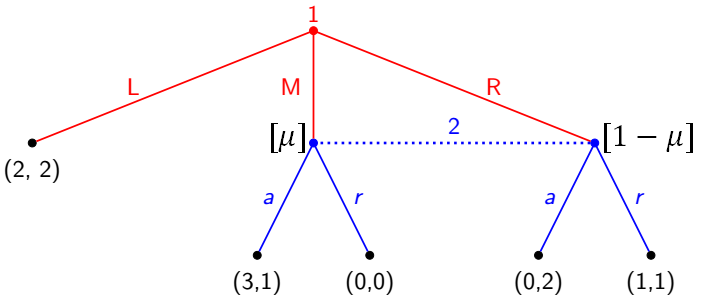
A belief μ is a function that assigns to every information set a probability measure on the set of histories in the information set

它为每个信息集分配一个概率测度，该测度定义在该信息集中的历史路径集合上

The probability is 1 for the information set of size 1

A behavior strategy β a collection of independent probability measure over the actions after information set

Beliefs affect optimal strategies: For 2, a is the best strategies iff 2 assigns a belief $μ(M)≤1/2$

Strategies affect reasonable beliefs: If 1 assigns to action (L,M,R) prob. (0.1,0.3,0.6), then Bayes rule requires the belief (1/3,2/3) of 2

What are reasonable beliefs if 1 select L with prob. 1

10.9.1 Two Requirements to Beliefs

Bayes consistency: beliefs are determined by Bayes’ law in information sets of positive probability; otherwise, beliefs are allowed to be arbitrary for 0 probability.

Consistency: beliefs are determined as a limit of case

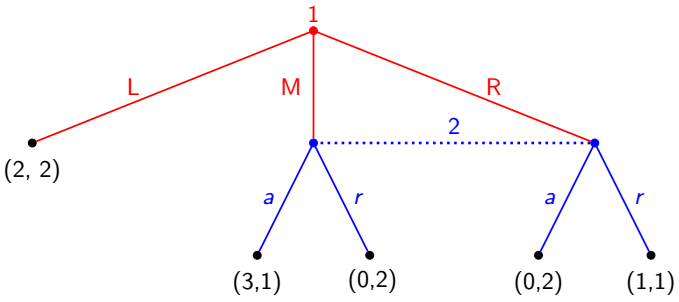
(L,M,R) with probability (1-ϵ,3ϵ/4,ϵ/4)

10.10 Assessment (评估)

An assessment is a pair $(\beta, \mu)$

• $\beta$ is an outcome of behavioral strategies
• $\mu$ is a belief system

An assessment $(\beta, \mu)$ is:

• Bayesian consistent if beliefs in information sets reached with positive probability are determined by Bayes’ law:

  $
  \mu_{(h,a)}(h,a) = \frac{\beta_{(h,a)}(h,a)}{\sum_a \beta_{(h,a)}(h,a)}
  $

  for every information set.

• Consistent if there is a sequence of Bayesian consistent assessments $(\beta^n, \mu^n)$ such that:

  $
  (\beta^n, \mu^n) \to (\beta, \mu) \quad \text{as} \quad n \to \infty,
  $

  and $\beta^n$ is a completely mixed strategy.

$(\beta, \mu)$ is consistent $\implies$ $(\beta, \mu)$ is Bayesian consistent.

10.10.1 example

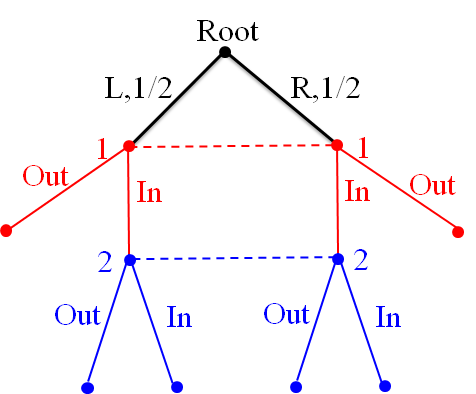
An assessment $(\beta, \mu)$ by a 4-tuple $(\beta_1, \beta_2, \mu_1, \mu_2) \in [0,1]^4$

• $\beta_1$ is the probability that 1 chooses In
• $\beta_2$ is the probability that 2 chooses In
• $\mu_1$ is the belief assigned to the left node in 1’ s info set
• $\mu_2$ is the belief assigned to the left node in 2’ s info set

Two cases:

i) If $\beta_1 \in (0,1]$, 2’ s information set is reached with positive probability. Bayes’ Law dictates that $\mu_1 = \mu_2 = \frac{1}{2}$.

$
(\beta_1, \beta_2, \mu_1, \mu_2) = (0,1] \times [0,1] \times \left\{ \frac{1}{2} \right\} \times \left\{ \frac{1}{2} \right\}
$

are Bayesian consistent.

ii) If $\beta_1 = 0$, then 2’ s information set is reached with zero probability and $\mu_2 \in [0,1]$.

$
(\beta_1, \beta_2, \mu_1, \mu_2) = \{ 0 \} \times [0,1] \times \left\{ \frac{1}{2} \right\} \times [0,1]
$

are Bayesian consistent.

Every complete outcome of behavioral strategies leads to $\mu_1 = \mu_2 = \frac{1}{2}$.

For 2’ s information set, both nodes are reached with equal probability.

Conclusion:

$
(\beta_1, \beta_2, \mu_1, \mu_2) = [0,1] \times [0,1] \times \left\{ \frac{1}{2} \right\} \times \left\{ \frac{1}{2} \right\}
$

are consistent.

10.11 Expected Payoffs in Information Sets

Fix assessment $(\beta, \mu)$ and information set $I_{ij}$ of player $i$. We consider the expected payoff of player $i$ on $I_{ij}$ as:

Given $I_{ij}$, the belief $\mu$ assigns probability over $I_{ij}$ with $\mu(h)$ for $h \in I_{ij}$.

e: Terminal history

For $h \in I_{ij}$, let $P(e|h, \beta)$ be the probability from $h$ to $e$ under the behavioral strategy $\beta$, and the payoff is $u_i(e)$.

The expected payoff for player $i$ in the information $I_{ij}$ w.r.t. $(\beta, \mu)$ is:

$
u_i(\beta_i, \beta_{-i} | I_{ij}, \mu) = \sum_{h \in I_{ij}} \mu(h) \left( \sum_e P(e | h, \beta) u_i(e) \right)
$